Difference between revisions of "Hausdorff dimension"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 2: | Line 2: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> F. Hausdorff, "Dimension and äusseres Mass" ''Math. Ann.'' , '''79''' (1918) pp. 157–179</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> W. Hurevicz, G. Wallman, "Dimension theory" , Princeton Univ. Press (1948)</TD></TR></table> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> F. Hausdorff, "Dimension and äusseres Mass" ''Math. Ann.'' , '''79''' (1918) pp. 157–179 {{MR|1511917}} {{ZBL|}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> W. Hurevicz, G. Wallman, "Dimension theory" , Princeton Univ. Press (1948) {{MR|}} {{ZBL|}} </TD></TR></table> |
| Line 12: | Line 12: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> K.J. Falconer, "The geometry of fractal sets" , Cambridge Univ. Press (1985)</TD></TR></table> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> K.J. Falconer, "The geometry of fractal sets" , Cambridge Univ. Press (1985) {{MR|0867284}} {{ZBL|0587.28004}} </TD></TR></table> |
Revision as of 11:59, 27 September 2012
A numerical invariant of metric spaces, introduced by F. Hausdorff in [1]. Let 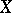 be a metric space. For real
be a metric space. For real 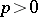 and
and 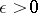 , let
, let 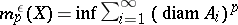 , where the lower bound is taken over all countable coverings
, where the lower bound is taken over all countable coverings 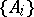 of
of 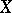 for which
for which 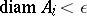 . The Hausdorff dimension of
. The Hausdorff dimension of 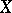 is defined as
is defined as 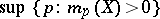 , where
, where 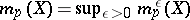 . The number thus defined depends on the metric on
. The number thus defined depends on the metric on 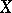 (on this, see also Metric dimension) and is, generally speaking, not an integer (for example, the Hausdorff dimension of the Cantor set is
(on this, see also Metric dimension) and is, generally speaking, not an integer (for example, the Hausdorff dimension of the Cantor set is 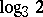 ). A topological invariant is, for example, the lower bound of the Hausdorff dimensions over all metrics on a given topological space
). A topological invariant is, for example, the lower bound of the Hausdorff dimensions over all metrics on a given topological space 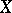 ; when
; when 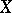 is compact, this invariant is the same as the Lebesgue dimension of
is compact, this invariant is the same as the Lebesgue dimension of 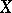 .
.
References
| [1] | F. Hausdorff, "Dimension and äusseres Mass" Math. Ann. , 79 (1918) pp. 157–179 MR1511917 |
| [2] | W. Hurevicz, G. Wallman, "Dimension theory" , Princeton Univ. Press (1948) |
Comments
The limit 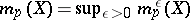 of the non-decreasing set
of the non-decreasing set 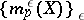 is called the Hausdorff measure of
is called the Hausdorff measure of 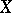 in dimension
in dimension 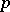 . There is then a unique
. There is then a unique 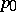 in the extended real line
in the extended real line 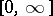 such that
such that 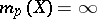 for
for 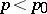 and
and 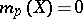 for
for 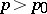 . This real number is the Hausdorff dimension of
. This real number is the Hausdorff dimension of 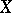 . It is also called the Hausdorff–Besicovitch dimension.
. It is also called the Hausdorff–Besicovitch dimension.
See also (the editorial comments to) Hausdorff measure for more material and references. The Hausdorff dimension is a basic notion in the theory of fractals, cf. also [a1].
References
| [a1] | K.J. Falconer, "The geometry of fractal sets" , Cambridge Univ. Press (1985) MR0867284 Zbl 0587.28004 |
Hausdorff dimension. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hausdorff_dimension&oldid=11884