Difference between revisions of "Elliptic partial differential equation"
From Encyclopedia of Mathematics
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 37: | Line 37: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> L.V. Hörmander, "The analysis of linear partial differential operators" , '''1''' , Springer (1983)</TD></TR></table> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> L.V. Hörmander, "The analysis of linear partial differential operators" , '''1''' , Springer (1983) {{MR|0717035}} {{MR|0705278}} {{ZBL|0521.35002}} {{ZBL|0521.35001}} </TD></TR></table> |
Revision as of 11:58, 27 September 2012
at a given point 
A partial differential equation of order 
,
 |
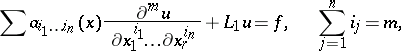such that 
is a differential operator of order less than 
, whose characteristic equation at 
,
 |
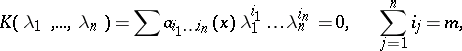has no real roots except 
.
For second-order equations the characteristic form is quadratic,
 |
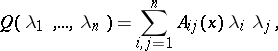and can be brought to the form
 |
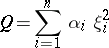by a non-singular affine transformation of the variables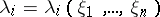 
, 
.
When all 
or all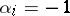 
, the equation is said to be of elliptic type.
A partial differential equation is said to be of elliptic type in its domain of definition if it is elliptic at every point of this domain.
An elliptic partial differential is called uniformly elliptic if there are positive numbers 
and 
such that
 |
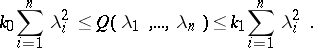For references see Differential equation, partial.
Comments
References
| [a1] | L.V. Hörmander, "The analysis of linear partial differential operators" , 1 , Springer (1983) MR0717035 MR0705278 Zbl 0521.35002 Zbl 0521.35001 |
How to Cite This Entry:
Elliptic partial differential equation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Elliptic_partial_differential_equation&oldid=12485
Elliptic partial differential equation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Elliptic_partial_differential_equation&oldid=12485
This article was adapted from an original article by A.B. Ivanov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article