Difference between revisions of "Bernstein theorem"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 4: | Line 4: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> S.N. [S.N. Bernshtein] Bernstein, "Über ein geometrisches Theorem und seine Anwendung auf die partiellen Differentialgleichungen vom elliptischen Typus" ''Math. Z.'' , '''26''' (1927) pp. 551–558 (Translated from French)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> J.C.C. Nitsche, "Vorlesungen über Minimalflächen" , Springer (1975)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> R. Osserman, "Minimal varieties" ''Bull. Amer. Math. Soc.'' , '''75''' (1969) pp. 1092–1120</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> R. Osserman, "A survey of minimal surfaces" , v. Nostrand (1969)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> A.T. Fomenko, "Plateau's problem" , Gordon & Breach (1987) (Translated from Russian)</TD></TR></table> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> S.N. [S.N. Bernshtein] Bernstein, "Über ein geometrisches Theorem und seine Anwendung auf die partiellen Differentialgleichungen vom elliptischen Typus" ''Math. Z.'' , '''26''' (1927) pp. 551–558 (Translated from French) {{MR|1544873}} {{ZBL|53.0670.01}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> J.C.C. Nitsche, "Vorlesungen über Minimalflächen" , Springer (1975) {{MR|0448224}} {{ZBL|0319.53003}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> R. Osserman, "Minimal varieties" ''Bull. Amer. Math. Soc.'' , '''75''' (1969) pp. 1092–1120 {{MR|0276875}} {{ZBL|0188.53801}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> R. Osserman, "A survey of minimal surfaces" , v. Nostrand (1969) {{MR|0256278}} {{ZBL|0209.52901}} </TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> A.T. Fomenko, "Plateau's problem" , Gordon & Breach (1987) (Translated from Russian) {{MR|}} {{ZBL|}} </TD></TR></table> |
| Line 12: | Line 12: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> E. Bombieri, E. de Giorgi, E. Giusti, "Minimal cones and the Bernstein theorem" ''Inventiones Math.'' , '''7''' (1969) pp. 243–269</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> S.N. Bernstein, "Sur une théorème de géometrie et ses applications aux équations dérivées partielles du type elliptique" ''Comm. Soc. Math. Kharkov'' , '''15''' (1915–1917) pp. 38–45</TD></TR></table> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> E. Bombieri, E. de Giorgi, E. Giusti, "Minimal cones and the Bernstein theorem" ''Inventiones Math.'' , '''7''' (1969) pp. 243–269 {{MR|}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> S.N. Bernstein, "Sur une théorème de géometrie et ses applications aux équations dérivées partielles du type elliptique" ''Comm. Soc. Math. Kharkov'' , '''15''' (1915–1917) pp. 38–45 {{MR|}} {{ZBL|}} </TD></TR></table> |
Revision as of 11:57, 27 September 2012
on minimal surfaces
If a minimal surface is given by the equation 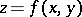 , where
, where 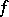 has continuous partial derivatives of the first and second orders for all real
has continuous partial derivatives of the first and second orders for all real  and
and 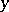 , then
, then 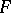 is a plane. A proof of this theorem, which is due to S.N. Bernstein [S.N. Bernshtein] [1], is a consequence of a more general theorem on the behaviour of surfaces with non-positive curvature. Various generalizations of Bernstein's theorem have been proposed, most of them being of the three following kinds: 1) Quantitative improvements; e.g. obtaining a priori estimates of the form
is a plane. A proof of this theorem, which is due to S.N. Bernstein [S.N. Bernshtein] [1], is a consequence of a more general theorem on the behaviour of surfaces with non-positive curvature. Various generalizations of Bernstein's theorem have been proposed, most of them being of the three following kinds: 1) Quantitative improvements; e.g. obtaining a priori estimates of the form 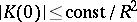 where
where 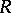 is the radius of the disc over which the minimal surface
is the radius of the disc over which the minimal surface 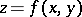 is defined and
is defined and 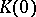 is the Gaussian curvature of the surface at the centre of the disc. 2) The search for other a priori geometric conditions under which the minimal surface would be of a specific kind — a plane, a catenoid, etc.; for instance, if the spherical image of a complete minimal surface contains no open set on the sphere, then such a minimal surface is a plane. 3) The generalization of Bernstein's theorem to minimal surfaces
is the Gaussian curvature of the surface at the centre of the disc. 2) The search for other a priori geometric conditions under which the minimal surface would be of a specific kind — a plane, a catenoid, etc.; for instance, if the spherical image of a complete minimal surface contains no open set on the sphere, then such a minimal surface is a plane. 3) The generalization of Bernstein's theorem to minimal surfaces 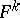 of dimension
of dimension 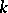 , located in a Euclidean space
, located in a Euclidean space 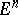 ; for example, if
; for example, if 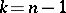 , any minimal surface over all
, any minimal surface over all  is uniquely determined if
is uniquely determined if 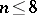 , and is a hyperplane, while if
, and is a hyperplane, while if 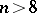 , there exist non-planar minimal surfaces; if
, there exist non-planar minimal surfaces; if 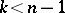 , then already for
, then already for  it is possible to find non-linear minimal surfaces
it is possible to find non-linear minimal surfaces 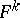 , defined over any
, defined over any  .
.
References
| [1] | S.N. [S.N. Bernshtein] Bernstein, "Über ein geometrisches Theorem und seine Anwendung auf die partiellen Differentialgleichungen vom elliptischen Typus" Math. Z. , 26 (1927) pp. 551–558 (Translated from French) MR1544873 Zbl 53.0670.01 |
| [2] | J.C.C. Nitsche, "Vorlesungen über Minimalflächen" , Springer (1975) MR0448224 Zbl 0319.53003 |
| [3] | R. Osserman, "Minimal varieties" Bull. Amer. Math. Soc. , 75 (1969) pp. 1092–1120 MR0276875 Zbl 0188.53801 |
| [4] | R. Osserman, "A survey of minimal surfaces" , v. Nostrand (1969) MR0256278 Zbl 0209.52901 |
| [5] | A.T. Fomenko, "Plateau's problem" , Gordon & Breach (1987) (Translated from Russian) |
Comments
As an important reference for the generalizations of Bernstein's theorem the paper of Bombieri–de Giorgi–Giusti [a1] can be quoted. The original of [1] is [a2].
References
| [a1] | E. Bombieri, E. de Giorgi, E. Giusti, "Minimal cones and the Bernstein theorem" Inventiones Math. , 7 (1969) pp. 243–269 |
| [a2] | S.N. Bernstein, "Sur une théorème de géometrie et ses applications aux équations dérivées partielles du type elliptique" Comm. Soc. Math. Kharkov , 15 (1915–1917) pp. 38–45 |
Bernstein theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bernstein_theorem&oldid=13184