Difference between revisions of "Signed measure"
(Importing text file) |
m (moved Charge to Signed measure: It is a more common terminology.) |
(No difference)
| |
Revision as of 21:35, 27 July 2012
generalized measure
An extended real-valued 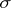 -additive set function that is defined on the
-additive set function that is defined on the 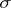 -algebra of Borel subsets of a domain
-algebra of Borel subsets of a domain 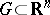 and that is finite on compact sets
and that is finite on compact sets 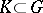 . The difference between two measures one of which is finite on
. The difference between two measures one of which is finite on 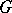 is a charge; conversely, all charges may be obtained in this way: for any charge
is a charge; conversely, all charges may be obtained in this way: for any charge  there exists a decomposition of
there exists a decomposition of 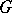 into two disjoint Borel sets
into two disjoint Borel sets  and
and 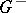 such that
such that 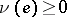 for
for 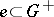 and
and 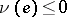 for
for 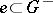 . The measures
. The measures 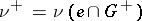 and
and 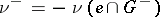 are independent of the choice of
are independent of the choice of 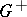 and
and 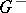 and are known respectively as the positive and negative variations of the charge
and are known respectively as the positive and negative variations of the charge  ; the measure
; the measure 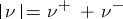 is called the total variation of
is called the total variation of  . With this notation, the so-called Hahn–Jordan decomposition:
. With this notation, the so-called Hahn–Jordan decomposition: 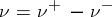 holds, so that the properties of charges may be phrased in terms of measure theory.
holds, so that the properties of charges may be phrased in terms of measure theory.
References
| [1] | N.S. Landkof, "Foundations of modern potential theory" , Springer (1972) (Translated from Russian) |
| [2] | P.R. Halmos, "Measure theory" , v. Nostrand (1950) |
Comments
A charge is also called a signed measure [a1], a real measure or a signed content. It can, more generally, be defined on a ring of subsets of a space  , or, alternatively, on a Riesz space of functions on
, or, alternatively, on a Riesz space of functions on  , see [a2].
, see [a2].
Any pair 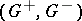 as above is called a Hahn decomposition of
as above is called a Hahn decomposition of  with respect to
with respect to  . The pair
. The pair 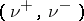 , defined above, is also called the Jordan decomposition of
, defined above, is also called the Jordan decomposition of  .
.
References
| [a1] | E. Hewitt, K.R. Stromberg, "Real and abstract analysis" , Springer (1965) |
| [a2] | K. Jacobs, "Measure and integral" , Acad. Press (1978) |
Signed measure. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Signed_measure&oldid=19071