Difference between revisions of "Wilson theorem"
(Importing text file) |
|||
| Line 7: | Line 7: | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> A.A. Bukhshtab, "Number theory" , Moscow (1966) (In Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> E. Trost, "Primzahlen" , Birkhäuser (1953)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> I.M. [I.M. Vinogradov] Winogradow, "Elemente der Zahlentheorie" , R. Oldenbourg (1956) (Translated from Russian)</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> A.A. Bukhshtab, "Number theory" , Moscow (1966) (In Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> E. Trost, "Primzahlen" , Birkhäuser (1953)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> I.M. [I.M. Vinogradov] Winogradow, "Elemente der Zahlentheorie" , R. Oldenbourg (1956) (Translated from Russian)</TD></TR></table> | ||
| − | + | [4] Amrik Singh Nimbran, ''Some Remarks on Wilson's Theorem'', 'The Mathematics Student',Indian Mathematical Society, | |
| − | + | Vol. 67, Nos. 1–4 (1998), 243–245 | |
====Comments==== | ====Comments==== | ||
Revision as of 14:43, 17 July 2012
Let 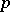 be a prime number. Then the number
be a prime number. Then the number 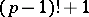 is divisible by
is divisible by 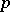 . The theorem was first formulated by E. Waring (1770) and is, according to him, due to J. Wilson. It was proved by J.L. Lagrange in 1771. A primality test for integers follows from Wilson's theorem: A natural number
. The theorem was first formulated by E. Waring (1770) and is, according to him, due to J. Wilson. It was proved by J.L. Lagrange in 1771. A primality test for integers follows from Wilson's theorem: A natural number  will be prime if and only if
will be prime if and only if
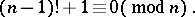 |
This test is not recommended for practical use, since the factorial involved rapidly becomes very large.
References
| [1] | A.A. Bukhshtab, "Number theory" , Moscow (1966) (In Russian) |
| [2] | E. Trost, "Primzahlen" , Birkhäuser (1953) |
| [3] | I.M. [I.M. Vinogradov] Winogradow, "Elemente der Zahlentheorie" , R. Oldenbourg (1956) (Translated from Russian) |
[4] Amrik Singh Nimbran, Some Remarks on Wilson's Theorem, 'The Mathematics Student',Indian Mathematical Society, Vol. 67, Nos. 1–4 (1998), 243–245
Comments
In fact, also the converse is true (and usually also called Wilson's theorem): Let 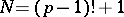 , with
, with 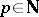 . Then
. Then  is divisible by
is divisible by 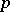 if and only if
if and only if 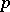 is a prime number.
is a prime number.
References
| [a1] | D. Shanks, "Solved and unsolved problems in number theory" , Chelsea, reprint (1978) |
| [a2] | M.R. Schroeder, "Number theory in science and communication" , Springer (1984) pp. 103 |
| [a3] | G.H. Hardy, E.M. Wright, "An introduction to the theory of numbers" , Clarendon Press (1960) pp. 68 |
Wilson theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Wilson_theorem&oldid=17357