Namespaces
Variants
Actions

Difference between pages "Hypocycloid" and "Laplace distribution"

From Encyclopedia of Mathematics
(Difference between pages)
Jump to: navigation, search
(Importing text file)
 
(→‎References: Feller: internal link)
 
Line 1: Line 1:
−
A plane curve which is the trajectory of a point on a circle rolling along a second circle while osculating it from inside. The parametric equations are
+
A continuous probability distribution with density
  
−
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h048/h048530/h0485301.png" /></td> </tr></table>
+
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l057/l057460/l0574601.png" /></td> </tr></table>
  
−
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h048/h048530/h0485302.png" /></td> </tr></table>
+
where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l057/l057460/l0574602.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l057/l057460/l0574603.png" />, is a shift parameter and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l057/l057460/l0574604.png" /> is a scale parameter. The density of the Laplace distribution is symmetric about the point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l057/l057460/l0574605.png" />, and the derivative of the density has a discontinuity at <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l057/l057460/l0574606.png" />. The characteristic function of the Laplace distribution with parameters <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l057/l057460/l0574607.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l057/l057460/l0574608.png" /> is
  
−
where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h048/h048530/h0485303.png" /> is the radius of the moving circle, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h048/h048530/h0485304.png" /> is the radius of the fixed circle and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h048/h048530/h0485305.png" /> is the angle between the radius vector of the centre of the moving circle with the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h048/h048530/h0485306.png" />-axis (assuming the trajectory passes through <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h048/h048530/h0485307.png" />). Depending on the size of the modulus <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h048/h048530/h0485308.png" />, hypocycloids of different forms are obtained. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h048/h048530/h0485309.png" /> is an integer, the curve consists of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h048/h048530/h04853010.png" /> non-intersecting branches (Fig. a). The points of return <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h048/h048530/h04853011.png" /> have polar coordinates <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h048/h048530/h04853012.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h048/h048530/h04853013.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h048/h048530/h04853014.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h048/h048530/h04853015.png" /> is irrational, the number of branches is infinite, and the point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h048/h048530/h04853016.png" /> does not return to its initial location; if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h048/h048530/h04853017.png" /> is rational, the hypocycloid is a closed algebraic curve. The arc length from the point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h048/h048530/h04853018.png" /> is
+
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l057/l057460/l0574609.png" /></td> </tr></table>
  
−
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h048/h048530/h04853019.png" /></td> </tr></table>
+
The Laplace distribution has finite moments of any order. In particular, its [[Mathematical expectation|mathematical expectation]] is <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l057/l057460/l05746010.png" /> and its variance (cf. [[Dispersion|Dispersion]]) is <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l057/l057460/l05746011.png" />.
  
−
The radius of the curvature is
+
The Laplace distribution was first introduced by P. Laplace [[#References|[1]]] and is often called the  "first law of Laplacefirst law of Laplace" , in contrast to the "second law of Laplacesecond law of Laplace" , as the [[Normal distribution|normal distribution]] is sometimes called. The Laplace distribution is also called the two-sided exponential distribution, on account of the fact that the Laplace distribution coincides with the distribution of the random variable
  
−
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h048/h048530/h04853020.png" /></td> </tr></table>
+
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l057/l057460/l05746012.png" /></td> </tr></table>
  
−
<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h048/h048530/h04853021.png" />.
+
where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l057/l057460/l05746013.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l057/l057460/l05746014.png" /> are independent random variables that have the same [[Exponential distribution|exponential distribution]] with density <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l057/l057460/l05746015.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l057/l057460/l05746016.png" />. The Laplace distribution with density <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l057/l057460/l05746017.png" /> and the [[Cauchy distribution|Cauchy distribution]] with density <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l057/l057460/l05746018.png" /> are related in the following way:
  
−
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/h048530a.gif" />
+
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l057/l057460/l05746019.png" /></td> </tr></table>
  
−
Figure: h048530a
+
and
  
−
If the point is not located on the rolling circle, but outside (or inside) it, the curve is said to be a lengthened (shortened) hypocycloid, or hypotrochoid (cf. [[Trochoid|Trochoid]]). If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h048/h048530/h04853022.png" /> the hypocycloid is a segment of a straight line; if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h048/h048530/h04853023.png" />, it is a [[Steiner curve|Steiner curve]]; if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h048/h048530/h04853024.png" />, it is an [[Astroid|astroid]]. Hypocycloids belong to the so-called cycloidal curves (cf. [[Cycloidal curve|Cycloidal curve]]).
+
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l057/l057460/l05746020.png" /></td> </tr></table>
  
 
====References====
 
====References====
−
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> A.A. Savelov,   "Planar curves" , Moscow  (1960)  (In Russian)</TD></TR></table>
+
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> P.S. Laplace, "Théorie analytique des probabilités", Paris (1812)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> W. Feller, [[Feller, "An introduction to probability theory and its  applications"|"An introduction to probability theory and its applications"]], '''2''', Wiley (1971)</TD></TR></table>
  
 +
====Comments====
  
−
 
−
====Comments====
 
−
Every hypocycloid which is generated by circles with radii <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h048/h048530/h04853025.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h048/h048530/h04853026.png" /> can also be generated by circles with radii <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h048/h048530/h04853027.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h048/h048530/h04853028.png" /> ([[#References|[a2]]], [[#References|[a3]]]). Hypocycloids, and more generally trochoids, play an important role in plane kinematics.
 
  
 
====References====
 
====References====
−
<table><TR><TD valign="top">[a1]</TD> <TD valign="top">  M. Berger,  "Geometry" , '''I''' , Springer  (1987)  pp. 273–276</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top">  K. Fladt,  "Analytische Geometrie spezieller ebener Kurven" , Akad. Verlagsgesell.  (1962)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top">  H.R. Müller,  "Kinematik" , de Gruyter (1963)</TD></TR></table>
+
<table><TR><TD valign="top">[a1]</TD> <TD valign="top">  E. Lukacs,  "Characteristic functions" , Griffin (1970)</TD></TR></table>

Revision as of 09:15, 4 May 2012

A continuous probability distribution with density

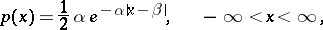where , , is a shift parameter and is a scale parameter. The density of the Laplace distribution is symmetric about the point , and the derivative of the density has a discontinuity at . The characteristic function of the Laplace distribution with parameters and is

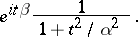The Laplace distribution has finite moments of any order. In particular, its mathematical expectation is 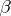and its variance (cf. Dispersion) is .

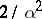The Laplace distribution was first introduced by P. Laplace [1] and is often called the "first law of Laplacefirst law of Laplace" , in contrast to the "second law of Laplacesecond law of Laplace" , as the normal distribution is sometimes called. The Laplace distribution is also called the two-sided exponential distribution, on account of the fact that the Laplace distribution coincides with the distribution of the random variable

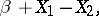where and 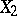are independent random variables that have the same exponential distribution with density , 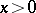. The Laplace distribution with density and the Cauchy distribution with density are related in the following way:

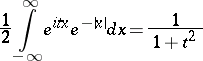and

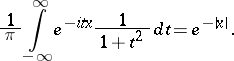References

[1] P.S. Laplace, "Théorie analytique des probabilités", Paris (1812)
[2] W. Feller, "An introduction to probability theory and its applications", 2, Wiley (1971)

Comments

References

[a1] E. Lukacs, "Characteristic functions" , Griffin (1970)
How to Cite This Entry:
Hypocycloid. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hypocycloid&oldid=14707
This article was adapted from an original article by D.D. Sokolov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article
Retrieved from "https://encyclopediaofmath.org/index.php?title=Hypocycloid&oldid=25936"