Difference between revisions of "Variation of Hodge structure"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 6: | Line 6: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1a]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1a]</TD> <TD valign="top"> P. Griffiths, "Periods of integrals on algebraic manifolds I" ''Amer. J. Math.'' , '''90''' (1968) pp. 568–626 {{MR|0229641}} {{ZBL|0169.52303}} </TD></TR><TR><TD valign="top">[a1b]</TD> <TD valign="top"> P. Griffiths, "Periods of integrals on algebraic manifolds II" ''Amer. J. Math.'' , '''90''' (1968) pp. 808–865 {{MR|0233825}} {{ZBL|0183.25501}} </TD></TR><TR><TD valign="top">[a1c]</TD> <TD valign="top"> P. Griffiths, "Periods of integrals on algebraic manifolds III" ''Publ. Math. IHES'' , '''38''' (1970) pp. 228–296 {{MR|0282990}} {{ZBL|0212.53503}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> P. Deligne, "Travaux de Griffiths" , ''Sem. Bourbaki Exp. 376'' , ''Lect. notes in math.'' , '''180''' , Springer (1970) pp. 213–235 {{MR|}} {{ZBL|0208.48601}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> W. Schmid, "Variation of Hodge structure: the singularities of the period mapping" ''Invent. Math.'' , '''22''' (1973) pp. 211–319 {{MR|0382272}} {{ZBL|0278.14003}} </TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> E. Cattani, A. Kaplan, W. Schmid, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096170/v09617050.png" /> and intersection cohomologies for a polarizable variation of Hodge structure" ''Invent. Math.'' , '''87''' (1987) pp. 217–252 {{MR|870728}} {{ZBL|0611.14006}} </TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> M. Kashiwara, T. Kawai, "The Poincaré lemma for variations of polarized Hodge structures" ''Publ. R.I.M.S. Kyoto Univ.'' , '''23''' (1987) pp. 345–407 {{MR|0890924}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> S. Zucker, "Hodge theory with degenerating coefficients: <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096170/v09617051.png" />-cohomology in the Poincaré metric" ''Ann. of Math.'' , '''109''' (1979) pp. 415–476 {{MR|534758}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> M. Saito, "Modules de Hodge polarisables" ''Publ. R.I.M.S. Kyoto Univ.'' , '''24''' (1988) pp. 849–995 {{MR|1000123}} {{ZBL|0691.14007}} </TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> J. Steenbrink, S. Zucker, "Variation of mixed Hodge structure, I" ''Invent. Math.'' , '''80''' (1985) pp. 489–542 {{MR|0791673}} {{MR|0791674}} {{ZBL|0626.14007}} </TD></TR><TR><TD valign="top">[a9]</TD> <TD valign="top"> M. Kashiwara, "A study of a variation of mixed Hodge structure" ''Publ. R.I.M.S. Kyoto Univ.'' , '''22''' (1986) pp. 991–1024 {{MR|866665}} {{ZBL|0621.14007}} </TD></TR><TR><TD valign="top">[a10]</TD> <TD valign="top"> M. Saito, "Mixed Hodge modules" ''Publ. R.I.M.S. Kyoto Univ.'' , '''26''' (1990) pp. 221–333 {{MR|1047741}} {{MR|1047415}} {{ZBL|0727.14004}} {{ZBL|0726.14007}} </TD></TR></table> |
Revision as of 17:02, 15 April 2012
A variation of Hodge structure of weight 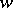 on a complex manifold
on a complex manifold 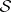 is a couple
is a couple 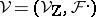 where
where 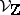 is a locally constant sheaf of finitely-generated Abelian groups on
is a locally constant sheaf of finitely-generated Abelian groups on 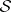 , and
, and 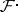 is a finite decreasing filtration of
is a finite decreasing filtration of 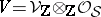 by holomorphic subbundles, subject to the following conditions: i) the flat connection
by holomorphic subbundles, subject to the following conditions: i) the flat connection  on
on 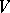 defined by
defined by 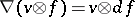 , for
, for  ,
, 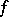 local sections of
local sections of 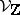 and
and 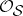 , respectively, satisfies
, respectively, satisfies 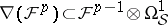 (Griffiths' transversality); ii) for each
(Griffiths' transversality); ii) for each 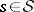 , the pair
, the pair 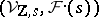 is a Hodge structure of weight
is a Hodge structure of weight 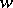 .
.
A polarization of a variation of Hodge structure 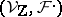 is a flat bilinear form
is a flat bilinear form 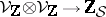 which induces a polarization of the Hodge structure
which induces a polarization of the Hodge structure 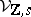 for each
for each 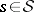 . Similar notions exist for
. Similar notions exist for 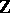 replaced by
replaced by 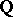 or
or 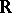 , [a2]. If
, [a2]. If 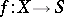 is a proper smooth morphism of algebraic varieties over
is a proper smooth morphism of algebraic varieties over 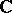 , then
, then 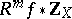 is the underlying local system of a polarizable variation of Hodge structure on
is the underlying local system of a polarizable variation of Hodge structure on 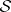 . By a result of A. Borel, for a polarized variation of Hodge structure on a complex manifold
. By a result of A. Borel, for a polarized variation of Hodge structure on a complex manifold 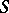 of the form
of the form 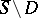 , where
, where 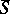 is compact and
is compact and 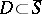 is a divisor with normal crossings, the monodromy around each local component of
is a divisor with normal crossings, the monodromy around each local component of 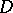 is quasi-unipotent [a3] (monodromy theorem). A polarized variation of Hodge structure over
is quasi-unipotent [a3] (monodromy theorem). A polarized variation of Hodge structure over  gives rise to a holomorphic period mapping from
gives rise to a holomorphic period mapping from 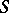 to a classifying space of Hodge structures (see Period mapping).
to a classifying space of Hodge structures (see Period mapping).
If 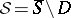 with
with 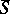 a compact Kähler manifold and
a compact Kähler manifold and 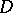 a divisor with normal crossings on
a divisor with normal crossings on 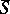 , then for a polarized variation of Hodge structure
, then for a polarized variation of Hodge structure 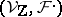 on
on 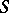 , the sheaf
, the sheaf 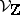 has a minimal extension to a perverse sheaf
has a minimal extension to a perverse sheaf  on
on 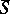 and
and 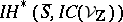 carries a pure Hodge structure [a4]–[a6]. In fact,
carries a pure Hodge structure [a4]–[a6]. In fact, 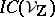 is part of a polarized Hodge module [a7]. Generalizations are the notions of variation of mixed Hodge structure [a8], [a9] and mixed Hodge module [a10].
is part of a polarized Hodge module [a7]. Generalizations are the notions of variation of mixed Hodge structure [a8], [a9] and mixed Hodge module [a10].
References
| [a1a] | P. Griffiths, "Periods of integrals on algebraic manifolds I" Amer. J. Math. , 90 (1968) pp. 568–626 MR0229641 Zbl 0169.52303 |
| [a1b] | P. Griffiths, "Periods of integrals on algebraic manifolds II" Amer. J. Math. , 90 (1968) pp. 808–865 MR0233825 Zbl 0183.25501 |
| [a1c] | P. Griffiths, "Periods of integrals on algebraic manifolds III" Publ. Math. IHES , 38 (1970) pp. 228–296 MR0282990 Zbl 0212.53503 |
| [a2] | P. Deligne, "Travaux de Griffiths" , Sem. Bourbaki Exp. 376 , Lect. notes in math. , 180 , Springer (1970) pp. 213–235 Zbl 0208.48601 |
| [a3] | W. Schmid, "Variation of Hodge structure: the singularities of the period mapping" Invent. Math. , 22 (1973) pp. 211–319 MR0382272 Zbl 0278.14003 |
| [a4] | E. Cattani, A. Kaplan, W. Schmid, "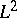 and intersection cohomologies for a polarizable variation of Hodge structure" Invent. Math. , 87 (1987) pp. 217–252 MR870728 Zbl 0611.14006 and intersection cohomologies for a polarizable variation of Hodge structure" Invent. Math. , 87 (1987) pp. 217–252 MR870728 Zbl 0611.14006 |
| [a5] | M. Kashiwara, T. Kawai, "The Poincaré lemma for variations of polarized Hodge structures" Publ. R.I.M.S. Kyoto Univ. , 23 (1987) pp. 345–407 MR0890924 |
| [a6] | S. Zucker, "Hodge theory with degenerating coefficients:  -cohomology in the Poincaré metric" Ann. of Math. , 109 (1979) pp. 415–476 MR534758 -cohomology in the Poincaré metric" Ann. of Math. , 109 (1979) pp. 415–476 MR534758 |
| [a7] | M. Saito, "Modules de Hodge polarisables" Publ. R.I.M.S. Kyoto Univ. , 24 (1988) pp. 849–995 MR1000123 Zbl 0691.14007 |
| [a8] | J. Steenbrink, S. Zucker, "Variation of mixed Hodge structure, I" Invent. Math. , 80 (1985) pp. 489–542 MR0791673 MR0791674 Zbl 0626.14007 |
| [a9] | M. Kashiwara, "A study of a variation of mixed Hodge structure" Publ. R.I.M.S. Kyoto Univ. , 22 (1986) pp. 991–1024 MR866665 Zbl 0621.14007 |
| [a10] | M. Saito, "Mixed Hodge modules" Publ. R.I.M.S. Kyoto Univ. , 26 (1990) pp. 221–333 MR1047741 MR1047415 Zbl 0727.14004 Zbl 0726.14007 |
Variation of Hodge structure. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Variation_of_Hodge_structure&oldid=15012