Difference between revisions of "Universal behaviour in dynamical systems"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 19: | Line 19: | ||
For <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095650/u09565024.png" /> (when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095650/u09565025.png" /> is sometimes called the Feigenbaum mapping), statement i) holds, but with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095650/u09565026.png" /> ranging over all non-negative integers, and ii) holds for each <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095650/u09565027.png" />; furthermore, the following analogue of iii) holds: | For <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095650/u09565024.png" /> (when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095650/u09565025.png" /> is sometimes called the Feigenbaum mapping), statement i) holds, but with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095650/u09565026.png" /> ranging over all non-negative integers, and ii) holds for each <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095650/u09565027.png" />; furthermore, the following analogue of iii) holds: | ||
| − | iv) (for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095650/u09565028.png" />) the closure of the orbit of the turning point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095650/u09565029.png" /> is a Cantor set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095650/u09565030.png" />, which is the asymptotic limit of every orbit not landing on one of the periodic orbits <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095650/u09565031.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095650/u09565032.png" />. The restricted mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095650/u09565033.png" /> is a minimal homeomorphism (the | + | iv) (for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095650/u09565028.png" />) the closure of the orbit of the turning point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095650/u09565029.png" /> is a Cantor set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095650/u09565030.png" />, which is the asymptotic limit of every orbit not landing on one of the periodic orbits <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095650/u09565031.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095650/u09565032.png" />. The restricted mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095650/u09565033.png" /> is a minimal homeomorphism (the "adding machine for chaos in a dynamical systemadding machine" ). |
| − | Finally, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095650/u09565034.png" /> is the threshold of | + | Finally, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095650/u09565034.png" /> is the threshold of "chaos" , in the following sense: |
v) for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095650/u09565035.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095650/u09565036.png" /> has infinitely many distinct periodic orbits, and positive topological entropy. | v) for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095650/u09565035.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095650/u09565036.png" /> has infinitely many distinct periodic orbits, and positive topological entropy. | ||
| − | Many features of this | + | Many features of this "topological" , or combinatorial picture were understood by early researchers in this area, specifically P.J. Myrberg [[#References|[a12]]] and N. Metropolis, M.L. Stein and P.R. Stein [[#References|[a13]]]. They recognized as well that the combinatorial structure of the periodic orbits <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095650/u09565037.png" /> is rigidly determined by the fact that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095650/u09565038.png" /> is unimodal (cf. [[#References|[a14]]]). In essence, the statements above can be formulated for any family of unimodal mappings (cf. ). In fact, the (weak) monotonicity of the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095650/u09565039.png" />'s, together with the fact that if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095650/u09565040.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095650/u09565041.png" /> must have periodic orbits of least period <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095650/u09565042.png" /> for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095650/u09565043.png" /> (some <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095650/u09565044.png" />) and no others, follows for any family of continuous mappings on the line from Sharkovskii's theorem [[#References|[a16]]], [[#References|[a2]]]; recent work has yielded a more general understanding of the combinatorial structure of periodic orbits for continuous mappings in dimension <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095650/u09565045.png" /> (cf. [[#References|[a1]]]). |
Coullet, Tresser and Feigenbaum added to the topological picture described above a number of analytic and geometric features: | Coullet, Tresser and Feigenbaum added to the topological picture described above a number of analytic and geometric features: | ||
| Line 37: | Line 37: | ||
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095650/u09565051.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095650/u09565051.png" /></td> </tr></table> | ||
| − | These statements, formulated for the particular family <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095650/u09565052.png" /> of quadratic mappings, are technically interesting, but not so striking. However, they observed that v)–vii) hold for a very broad class of unimodal one-parameter families, subject only to trivial | + | These statements, formulated for the particular family <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095650/u09565052.png" /> of quadratic mappings, are technically interesting, but not so striking. However, they observed that v)–vii) hold for a very broad class of unimodal one-parameter families, subject only to trivial "fullness" conditions (essentially that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095650/u09565053.png" /> has only finitely many periodic orbits while <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095650/u09565054.png" /> has positive entropy) and smoothness (essentially that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095650/u09565055.png" /> is <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095650/u09565056.png" /> and each <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095650/u09565057.png" /> has a non-degenerate critical point). And, sensationally, the constants <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095650/u09565058.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095650/u09565059.png" /> are independent of the family <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095650/u09565060.png" />. |
In [[#References|[a6]]] and | In [[#References|[a6]]] and | ||
| Line 43: | Line 43: | ||
these assertions were reduced, using ideas from renormalization theory, to certain technical conjectures concerning a doubling operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095650/u09565061.png" /> acting on an appropriate function space. O. Lanford | these assertions were reduced, using ideas from renormalization theory, to certain technical conjectures concerning a doubling operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095650/u09565061.png" /> acting on an appropriate function space. O. Lanford | ||
| − | (cf. also [[#References|[a3]]], [[#References|[a5]]]) gave a rigorous, computer-assisted proof of the basic conjecture, that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095650/u09565062.png" /> has a saddle-type fixed point with one characteristic multiplier <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095650/u09565063.png" /> (the same as in vi)) and stable manifold of codimension <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095650/u09565064.png" />. D. Sullivan [[#References|[a17]]] showed the uniqueness of this fixed point in the space of | + | (cf. also [[#References|[a3]]], [[#References|[a5]]]) gave a rigorous, computer-assisted proof of the basic conjecture, that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095650/u09565062.png" /> has a saddle-type fixed point with one characteristic multiplier <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095650/u09565063.png" /> (the same as in vi)) and stable manifold of codimension <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095650/u09565064.png" />. D. Sullivan [[#References|[a17]]] showed the uniqueness of this fixed point in the space of "quadratic-like" mappings. The final conjecture, concerning transversality of the stable manifold with certain bifurcation submanifolds, remains unproved. Recently, Sullivan , introducing a number of new ideas, has circumvented this difficulty and provided a rather complete theory of universal features for families of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095650/u09565065.png" /> unimodal mappings. In particular, the asymptotic geometry of the Cantor set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095650/u09565066.png" /> (for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095650/u09565067.png" />) and of analogous sets appearing at other "threshold" parameter values (the "infinitely renormalizable mappings of bounded type" ) is universal; for example, the set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095650/u09565068.png" /> always has [[Hausdorff dimension|Hausdorff dimension]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095650/u09565069.png" />. Full expositions of this theory are provided in [[#References|[a18]]] and [[#References|[a7]]]. |
These ideas have been applied as well to circle diffeomorphisms [[#References|[a10]]], | These ideas have been applied as well to circle diffeomorphisms [[#References|[a10]]], | ||
| Line 50: | Line 50: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> Ll. Alsedà, J. Llibre, M. Misiurewicz, "Combinatorial dynamics and entropy in one dimension" (to appear)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> L. Block, J. Guckenheimer, M. Misiurewicz, L.-S. Young, "Periodic points and topological entropy of one dimensional maps" Z. Nitecki (ed.) C. Robinson (ed.) , ''Global theory of dynamical systems (Proc. Northwestern Univ., 1979)'' , ''Lect. notes in math.'' , '''819''' , Springer (1980) pp. 18–34 {{MR|0591173}} {{ZBL|0447.58028}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> M. Campanino, H. Epstein, D. Ruelle, "On the existence of Feigenbaum's fixed point" ''Comm. Math. Phys.'' , '''79''' (1981) pp. 261–302 {{MR|612250}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> P. Collet, J.-P. Eckmann, H. Koch, "On universality for area-preserving maps of the plane" ''Physica'' , '''3D''' (1981) pp. 457–467 {{MR|0631180}} {{ZBL|1194.37050}} </TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> P. Collet, J.-P. Eckmann, O. Lanford, "Universal properties of maps on an interval" ''Comm. Math. Phys.'' , '''76''' (1980) pp. 211–254 {{MR|0588048}} {{ZBL|0455.58024}} </TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> P. Coullet, C. Tresser, "Itérations d'endomorphismes et groupe de rénormalisation" ''J. Phys.'' , '''C5''' (1978) pp. 25–28 {{MR|0512110}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> W. de Mello, S. van Strien, "One-dimensional dynamics" (to appear)</TD></TR><TR><TD valign="top">[a8a]</TD> <TD valign="top"> M. Feigenbaum, "Quantitative universality for a class of non-linear transformations" ''J. Stat. Phys.'' , '''19''' (1978) pp. 25–52 {{MR|501179}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a8b]</TD> <TD valign="top"> M. Feigenbaum, "The universal metric properties of a non-linear transformation" ''J. Stat. Phys.'' , '''21''' (1979) pp. 669–706 {{MR|555919}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a9a]</TD> <TD valign="top"> L. Jonker, D. Rand, "Bifurcations in one dimension" ''Invent. Math.'' , '''62''' (1981) pp. 347–365 {{MR|0608525}} {{MR|0604832}} {{ZBL|0475.58015}} </TD></TR><TR><TD valign="top">[a9b]</TD> <TD valign="top"> L. Jonker, D. Rand, "Bifurcations in one dimension" ''Invent. Math.'' , '''63''' (1981) pp. 1–16 {{MR|0608525}} {{MR|0604832}} {{ZBL|0475.58015}} </TD></TR><TR><TD valign="top">[a10]</TD> <TD valign="top"> L. Jonker, D. Rand, "Universal properties of maps of the circle with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095650/u09565070.png" />-singularities" ''Comm. Math. Phys.'' , '''90''' (1983) pp. 273–292 {{MR|714439}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a11a]</TD> <TD valign="top"> O. Lanford, "A computer-assisted proof of the Feigenbaum conjectures" ''Bull. Amer. Math. Soc.'' , '''6''' (1982) pp. 427–434 {{MR|0648529}} {{ZBL|0487.58017}} </TD></TR><TR><TD valign="top">[a11b]</TD> <TD valign="top"> O.E. Lanford, "Computer assisted proofs in analysis" A.M. Gleason (ed.) , ''Proc. Internat. Congress Mathematicians (Berkeley, 1986)'' , Amer. Math. Soc. (1987) pp. 1385–1394 {{MR|0934342}} {{ZBL|0676.65039}} </TD></TR><TR><TD valign="top">[a12]</TD> <TD valign="top"> P.J. Myrberg, "Sur l'iteration des polynomes réels quadratiques" ''J. Math. Pures Appl.'' , '''41''' (1962) pp. 339–351 {{MR|0161968}} {{ZBL|0106.04703}} </TD></TR><TR><TD valign="top">[a13]</TD> <TD valign="top"> N. Metropolis, M.L. Stein, P.R. Stein, "On finite limit sets for transformations on the unit interval" ''J. Comb. Theory'' , '''15A''' (1973) pp. 25–44 {{MR|0316636}} {{ZBL|0259.26003}} </TD></TR><TR><TD valign="top">[a14]</TD> <TD valign="top"> W. Thurston, "On iterated maps of the interval" J.C. Alexander (ed.) , ''Dynamical Systems (Proc. Maryland, 1986–7)'' , ''Lect. notes in math.'' , '''1342''' , Springer (1988) pp. 465–563 {{MR|0970571}} {{ZBL|0664.58015}} </TD></TR><TR><TD valign="top">[a15a]</TD> <TD valign="top"> D. Rand, "Universality and renormalization in dynamical systems" T. Bedford (ed.) J. W. Swift (ed.) , ''New directions in dynamical systems'' , Cambridge Univ. Press (1987) pp. 1–56</TD></TR><TR><TD valign="top">[a15b]</TD> <TD valign="top"> D. Rand, "Global phase space universality, smooth conjugacies and renormalisation: the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095650/u09565071.png" /> case." ''Nonlinearity'' , '''1''' (1988) pp. 181–202 {{MR|928952}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a16]</TD> <TD valign="top"> A.N. Sharkovskii, "Coexistence of cycles of a continuous map of the line into itself" ''Ukrain. Mat. Zh.'' , '''16''' (1964) pp. 61–71 (In Russian) {{MR|1415876}} {{MR|1361914}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a17]</TD> <TD valign="top"> D. Sullivan, "Quasiconformal homeomorphisms in dynamics, topology and geometry" A.M. Gleason (ed.) , ''Proc. Internat. Congress Mathematicians (Berkeley, 1986)'' , Amer. Math. Soc. (1987) pp. 1216–1228 {{MR|0934326}} {{ZBL|0698.58030}} </TD></TR><TR><TD valign="top">[a18]</TD> <TD valign="top"> D. Sullivan, "Bounds, quadratic differentials, and renormalization conjectures" , ''Centennial Publ.'' , '''2''' , Amer. Math. Soc. (1991) {{MR|1184622}} {{ZBL|0936.37016}} </TD></TR></table> |
Revision as of 17:02, 15 April 2012
In the late 1970's, P. Coullet and C. Tresser [a6] and M. Feigenbaum
independently found striking, unexpected features of the transition from simple to chaotic dynamics in one-dimensional dynamical systems (cf. also Routes to chaos). By the example of the family of quadratic mappings  acting (for
acting (for 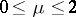 ) on the interval
) on the interval 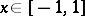 , the period-doubling scenario is recalled here. For
, the period-doubling scenario is recalled here. For 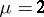 ,
, 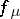 has periodic points of every (least) period. Let
has periodic points of every (least) period. Let  be the infimum of parameter values
be the infimum of parameter values 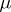 for which
for which 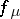 has a periodic orbit of least period
has a periodic orbit of least period  . Then
. Then
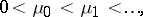 |
and
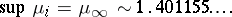 |
For 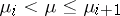 , the dynamics of
, the dynamics of 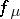 is described by statements i)–iii) below.
is described by statements i)–iii) below.
i) 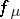 has precisely one periodic orbit
has precisely one periodic orbit 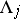 of (least) period
of (least) period 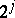 for each
for each 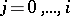 , and no other periodic orbits;
, and no other periodic orbits;
ii) any pair of adjacent points in 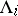 is separated by a unique point in
is separated by a unique point in 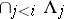 ;
;
iii) with the exception of the (countably many) orbits which land on some 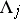 ,
, 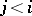 , and stay there, every
, and stay there, every 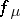 -orbit tends asymptotically to
-orbit tends asymptotically to 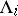 .
.
For 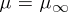 (when
(when 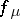 is sometimes called the Feigenbaum mapping), statement i) holds, but with
is sometimes called the Feigenbaum mapping), statement i) holds, but with 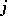 ranging over all non-negative integers, and ii) holds for each
ranging over all non-negative integers, and ii) holds for each 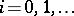 ; furthermore, the following analogue of iii) holds:
; furthermore, the following analogue of iii) holds:
iv) (for 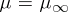 ) the closure of the orbit of the turning point
) the closure of the orbit of the turning point  is a Cantor set
is a Cantor set 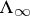 , which is the asymptotic limit of every orbit not landing on one of the periodic orbits
, which is the asymptotic limit of every orbit not landing on one of the periodic orbits 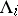 ,
, 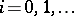 . The restricted mapping
. The restricted mapping 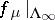 is a minimal homeomorphism (the "adding machine for chaos in a dynamical systemadding machine" ).
is a minimal homeomorphism (the "adding machine for chaos in a dynamical systemadding machine" ).
Finally, 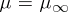 is the threshold of "chaos" , in the following sense:
is the threshold of "chaos" , in the following sense:
v) for 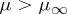 ,
, 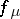 has infinitely many distinct periodic orbits, and positive topological entropy.
has infinitely many distinct periodic orbits, and positive topological entropy.
Many features of this "topological" , or combinatorial picture were understood by early researchers in this area, specifically P.J. Myrberg [a12] and N. Metropolis, M.L. Stein and P.R. Stein [a13]. They recognized as well that the combinatorial structure of the periodic orbits  is rigidly determined by the fact that
is rigidly determined by the fact that 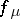 is unimodal (cf. [a14]). In essence, the statements above can be formulated for any family of unimodal mappings (cf. ). In fact, the (weak) monotonicity of the
is unimodal (cf. [a14]). In essence, the statements above can be formulated for any family of unimodal mappings (cf. ). In fact, the (weak) monotonicity of the  's, together with the fact that if
's, together with the fact that if 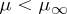 , then
, then  must have periodic orbits of least period
must have periodic orbits of least period  for
for 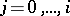 (some
(some 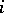 ) and no others, follows for any family of continuous mappings on the line from Sharkovskii's theorem [a16], [a2]; recent work has yielded a more general understanding of the combinatorial structure of periodic orbits for continuous mappings in dimension
) and no others, follows for any family of continuous mappings on the line from Sharkovskii's theorem [a16], [a2]; recent work has yielded a more general understanding of the combinatorial structure of periodic orbits for continuous mappings in dimension 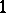 (cf. [a1]).
(cf. [a1]).
Coullet, Tresser and Feigenbaum added to the topological picture described above a number of analytic and geometric features:
vi) the convergence 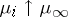 is asymptotically geometric:
is asymptotically geometric:
 |
vii) the periodic orbits scale: let 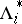 denote the orbit
denote the orbit 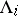 for
for  ; then
; then
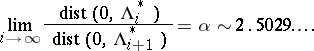 |
These statements, formulated for the particular family 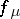 of quadratic mappings, are technically interesting, but not so striking. However, they observed that v)–vii) hold for a very broad class of unimodal one-parameter families, subject only to trivial "fullness" conditions (essentially that
of quadratic mappings, are technically interesting, but not so striking. However, they observed that v)–vii) hold for a very broad class of unimodal one-parameter families, subject only to trivial "fullness" conditions (essentially that  has only finitely many periodic orbits while
has only finitely many periodic orbits while 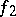 has positive entropy) and smoothness (essentially that
has positive entropy) and smoothness (essentially that  is
is 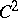 and each
and each  has a non-degenerate critical point). And, sensationally, the constants
has a non-degenerate critical point). And, sensationally, the constants 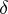 and
and 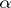 are independent of the family
are independent of the family 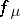 .
.
In [a6] and
these assertions were reduced, using ideas from renormalization theory, to certain technical conjectures concerning a doubling operator 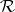 acting on an appropriate function space. O. Lanford
acting on an appropriate function space. O. Lanford
(cf. also [a3], [a5]) gave a rigorous, computer-assisted proof of the basic conjecture, that 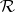 has a saddle-type fixed point with one characteristic multiplier
has a saddle-type fixed point with one characteristic multiplier  (the same as in vi)) and stable manifold of codimension
(the same as in vi)) and stable manifold of codimension  . D. Sullivan [a17] showed the uniqueness of this fixed point in the space of "quadratic-like" mappings. The final conjecture, concerning transversality of the stable manifold with certain bifurcation submanifolds, remains unproved. Recently, Sullivan , introducing a number of new ideas, has circumvented this difficulty and provided a rather complete theory of universal features for families of
. D. Sullivan [a17] showed the uniqueness of this fixed point in the space of "quadratic-like" mappings. The final conjecture, concerning transversality of the stable manifold with certain bifurcation submanifolds, remains unproved. Recently, Sullivan , introducing a number of new ideas, has circumvented this difficulty and provided a rather complete theory of universal features for families of 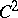 unimodal mappings. In particular, the asymptotic geometry of the Cantor set
unimodal mappings. In particular, the asymptotic geometry of the Cantor set  (for
(for 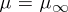 ) and of analogous sets appearing at other "threshold" parameter values (the "infinitely renormalizable mappings of bounded type" ) is universal; for example, the set
) and of analogous sets appearing at other "threshold" parameter values (the "infinitely renormalizable mappings of bounded type" ) is universal; for example, the set  always has Hausdorff dimension
always has Hausdorff dimension 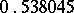 . Full expositions of this theory are provided in [a18] and [a7].
. Full expositions of this theory are provided in [a18] and [a7].
These ideas have been applied as well to circle diffeomorphisms [a10],
and area-preserving planar diffeomorphisms [a4], .
References
| [a1] | Ll. Alsedà, J. Llibre, M. Misiurewicz, "Combinatorial dynamics and entropy in one dimension" (to appear) |
| [a2] | L. Block, J. Guckenheimer, M. Misiurewicz, L.-S. Young, "Periodic points and topological entropy of one dimensional maps" Z. Nitecki (ed.) C. Robinson (ed.) , Global theory of dynamical systems (Proc. Northwestern Univ., 1979) , Lect. notes in math. , 819 , Springer (1980) pp. 18–34 MR0591173 Zbl 0447.58028 |
| [a3] | M. Campanino, H. Epstein, D. Ruelle, "On the existence of Feigenbaum's fixed point" Comm. Math. Phys. , 79 (1981) pp. 261–302 MR612250 |
| [a4] | P. Collet, J.-P. Eckmann, H. Koch, "On universality for area-preserving maps of the plane" Physica , 3D (1981) pp. 457–467 MR0631180 Zbl 1194.37050 |
| [a5] | P. Collet, J.-P. Eckmann, O. Lanford, "Universal properties of maps on an interval" Comm. Math. Phys. , 76 (1980) pp. 211–254 MR0588048 Zbl 0455.58024 |
| [a6] | P. Coullet, C. Tresser, "Itérations d'endomorphismes et groupe de rénormalisation" J. Phys. , C5 (1978) pp. 25–28 MR0512110 |
| [a7] | W. de Mello, S. van Strien, "One-dimensional dynamics" (to appear) |
| [a8a] | M. Feigenbaum, "Quantitative universality for a class of non-linear transformations" J. Stat. Phys. , 19 (1978) pp. 25–52 MR501179 |
| [a8b] | M. Feigenbaum, "The universal metric properties of a non-linear transformation" J. Stat. Phys. , 21 (1979) pp. 669–706 MR555919 |
| [a9a] | L. Jonker, D. Rand, "Bifurcations in one dimension" Invent. Math. , 62 (1981) pp. 347–365 MR0608525 MR0604832 Zbl 0475.58015 |
| [a9b] | L. Jonker, D. Rand, "Bifurcations in one dimension" Invent. Math. , 63 (1981) pp. 1–16 MR0608525 MR0604832 Zbl 0475.58015 |
| [a10] | L. Jonker, D. Rand, "Universal properties of maps of the circle with  -singularities" Comm. Math. Phys. , 90 (1983) pp. 273–292 MR714439 -singularities" Comm. Math. Phys. , 90 (1983) pp. 273–292 MR714439 |
| [a11a] | O. Lanford, "A computer-assisted proof of the Feigenbaum conjectures" Bull. Amer. Math. Soc. , 6 (1982) pp. 427–434 MR0648529 Zbl 0487.58017 |
| [a11b] | O.E. Lanford, "Computer assisted proofs in analysis" A.M. Gleason (ed.) , Proc. Internat. Congress Mathematicians (Berkeley, 1986) , Amer. Math. Soc. (1987) pp. 1385–1394 MR0934342 Zbl 0676.65039 |
| [a12] | P.J. Myrberg, "Sur l'iteration des polynomes réels quadratiques" J. Math. Pures Appl. , 41 (1962) pp. 339–351 MR0161968 Zbl 0106.04703 |
| [a13] | N. Metropolis, M.L. Stein, P.R. Stein, "On finite limit sets for transformations on the unit interval" J. Comb. Theory , 15A (1973) pp. 25–44 MR0316636 Zbl 0259.26003 |
| [a14] | W. Thurston, "On iterated maps of the interval" J.C. Alexander (ed.) , Dynamical Systems (Proc. Maryland, 1986–7) , Lect. notes in math. , 1342 , Springer (1988) pp. 465–563 MR0970571 Zbl 0664.58015 |
| [a15a] | D. Rand, "Universality and renormalization in dynamical systems" T. Bedford (ed.) J. W. Swift (ed.) , New directions in dynamical systems , Cambridge Univ. Press (1987) pp. 1–56 |
| [a15b] | D. Rand, "Global phase space universality, smooth conjugacies and renormalisation: the 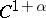 case." Nonlinearity , 1 (1988) pp. 181–202 MR928952 case." Nonlinearity , 1 (1988) pp. 181–202 MR928952 |
| [a16] | A.N. Sharkovskii, "Coexistence of cycles of a continuous map of the line into itself" Ukrain. Mat. Zh. , 16 (1964) pp. 61–71 (In Russian) MR1415876 MR1361914 |
| [a17] | D. Sullivan, "Quasiconformal homeomorphisms in dynamics, topology and geometry" A.M. Gleason (ed.) , Proc. Internat. Congress Mathematicians (Berkeley, 1986) , Amer. Math. Soc. (1987) pp. 1216–1228 MR0934326 Zbl 0698.58030 |
| [a18] | D. Sullivan, "Bounds, quadratic differentials, and renormalization conjectures" , Centennial Publ. , 2 , Amer. Math. Soc. (1991) MR1184622 Zbl 0936.37016 |
Universal behaviour in dynamical systems. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Universal_behaviour_in_dynamical_systems&oldid=12254