Kähler-Einstein manifold

A complex manifold carrying a Kähler–Einstein metric. By the uniqueness property of Kähler–Einstein metrics (see [a2], [a4]), the concept of a Kähler–Einstein manifold provides a very natural tool in studying the moduli space of compact complex manifolds.

Examples.

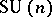1) Calabi–Yau manifolds. Any compact connected Kähler manifold of complex dimension with holonomy in is called a Calabi–Yau manifold. A Fermat quintic in 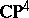with a natural Ricci-flat Kähler metric is a typical example of a Calabi–Yau threefold. Interesting subjects, such as mirror symmetry, have been studied for Calabi–Yau threefolds.

2) More generally, Ricci-flat Kähler manifolds are Kähler–Einstein manifolds (cf. also Ricci curvature). For instance, hyper-Kähler manifolds, characterized as 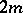-dimensional (possibly non-compact) Kähler manifolds with holonomy in 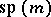, are Ricci-flat Kähler manifolds (see [a1], [a3]). An ALE gravitational instanton, obtained typically as a minimal resolution of an isolated quotient singularity in 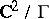, has the structure of a hyper-Kähler manifold. A K3-surface (cf. Surface, K3) is a compact hyper-Kähler manifold.

3) Kähler C-spaces. A compact simply connected homogeneous Kähler manifold, called a Kähler C-space, carries a Kähler–Einstein metric with positive scalar curvature and has the structure of a Kähler–Einstein manifold.

4) A twistor space of a quaternionic Kähler manifold with positive scalar curvature has the natural structure of a Kähler–Einstein manifold with positive scalar curvature (see [a3]).

5) Among the almost-homogeneous Kähler manifolds (cf. [a1]), the hypersurfaces in 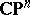and the del Pezzo surfaces (cf. [a5], [a6] or Cubic hypersurface), there are numerous examples of Kähler–Einstein manifolds with positive scalar curvature.

6) Any complex manifold covered by a bounded homogeneous domain in 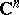endowed with a Bergman metric (cf. also Hyperbolic metric) is a Kähler–Einstein manifold with negative scalar curvature. More generally, a compact complex manifold 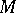with 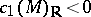naturally has the structure of a Kähler–Einstein manifold with negative scalar curvature.

Generalization.

A compact complex surface with quotient singularities obtained from a minimal algebraic surface of general type by blowing down 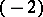-curves has the structure of a Kähler–Einstein orbifold, which is a slight generalization of the notion of a Kähler–Einstein manifold.

General references for Kähler–Einstein manifolds are [a1], [a2] and [a4].

References

[a1]	A.L. Besse, "Einstein manifolds" , Springer (1987) MR0867684 Zbl 0613.53001
[a2]	T. Ochiai, et al., "Kähler metrics and moduli spaces" , Adv. Stud. Pure Math. , 18–II , Kinokuniya (1990)
[a3]	S.M. Salamon, "Quaternionic Kähler manifolds" Invent. Math. , 67 (1987) pp. 175–203
[a4]	Y.-T. Siu, "Lectures on Hermitian–Einstein metrics for stable bundles and Kähler–Einstein metrics" , Birkhäuser (1987)
[a5]	G. Tian, "Kähler–Einstein metrics on certain Kähler manifolds with 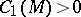" Invent. Math. , 89 (1987) pp. 225–246
[a6]	G. Tian, S.-T. Yau, "Kähler–Einstein metrics on complex surfaces with 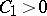" Comm. Math. Phys. , 112 (1987) pp. 175–203