Difference between revisions of "Finitely-determined function"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 14: | Line 14: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> S.C. Kleene, "Representation of events in nerve nets and finite automata" , ''Automata studies'' , '''34''' , Princeton Univ. Press (1956) pp. 3–41 {{MR|0077478}} {{ZBL|}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> S.V. Yablonskii, "Introduction to discrete mathematics" , Moscow (1986) (In Russian) {{MR|0911107}} {{ZBL|}} </TD></TR></table> |
| Line 21: | Line 21: | ||
(Finitely-) determined functions are also called (finite) sequential machine mappings or Mealy mappings. They are a special case of gsm-mappings, for which condition 1) above is not required. | (Finitely-) determined functions are also called (finite) sequential machine mappings or Mealy mappings. They are a special case of gsm-mappings, for which condition 1) above is not required. | ||
| − | Instead of | + | Instead of "remainder function" one also uses derivative. |
A rather different notion of finite determinacy of functions occurs in differential topology. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040340/f04034079.png" /> be a smooth function taking <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040340/f04034080.png" /> to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040340/f04034081.png" />. Roughly, a function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040340/f04034082.png" /> is finitely determined at <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040340/f04034083.png" /> if up to local diffeomorphisms of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040340/f04034084.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040340/f04034085.png" /> it is uniquely determined near 0 by the terms of order <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040340/f04034086.png" /> of its Taylor series at <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040340/f04034087.png" />; it is then said to be <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040340/f04034088.png" />-determined. The precise notions involve germs (cf. [[Germ|Germ]]) of functions and mappings. Cf. [[Singularities of differentiable mappings|Singularities of differentiable mappings]] for more details (in a more general setting) and for related notions such as stable germs of differentiable mappings, singularities of finite type, etc. | A rather different notion of finite determinacy of functions occurs in differential topology. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040340/f04034079.png" /> be a smooth function taking <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040340/f04034080.png" /> to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040340/f04034081.png" />. Roughly, a function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040340/f04034082.png" /> is finitely determined at <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040340/f04034083.png" /> if up to local diffeomorphisms of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040340/f04034084.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040340/f04034085.png" /> it is uniquely determined near 0 by the terms of order <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040340/f04034086.png" /> of its Taylor series at <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040340/f04034087.png" />; it is then said to be <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040340/f04034088.png" />-determined. The precise notions involve germs (cf. [[Germ|Germ]]) of functions and mappings. Cf. [[Singularities of differentiable mappings|Singularities of differentiable mappings]] for more details (in a more general setting) and for related notions such as stable germs of differentiable mappings, singularities of finite type, etc. | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> S. Ginsburg, "The mathematical theory of context-free languages" , McGraw-Hill (1965) {{MR|0211815}} {{ZBL|0195.02301}} {{ZBL|0184.28401}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> J.E. Hopcroft, J.D. Ulman, "Introduction to automata theory, languages and computation" , Addison-Wesley (1979) {{MR|0645539}} {{ZBL|0426.68001}} </TD></TR></table> |
Revision as of 16:57, 15 April 2012
A lexical function characterizing the behaviour of a finite automaton (cf. Automaton, finite). (A function is called lexical if its domain of definition and range of values are sets of words or superwords.)
Suppose that 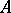 is an alphabet. Let
is an alphabet. Let 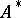 denote the set of all words, and
denote the set of all words, and 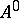 the set of all words or the set of all superwords over
the set of all words or the set of all superwords over 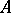 . A function
. A function 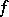 mapping
mapping 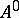 into
into 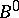 , where
, where 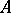 and
and 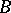 are any finite alphabets, is called a determined function if it satisfies the following two conditions:
are any finite alphabets, is called a determined function if it satisfies the following two conditions:
1) for any 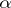 in
in 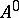 , the length of
, the length of 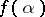 is equal to the length of
is equal to the length of 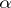 ; and
; and
2) if 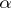 is a word of length
is a word of length 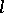 and
and 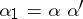 ,
, 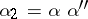 , where
, where 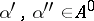 , then the values
, then the values  and
and 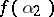 have the same beginnings of length
have the same beginnings of length 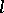 .
.
If a determined function 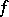 is defined on the set
is defined on the set 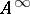 of all superwords over
of all superwords over 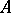 then, by conditions 1) and 2), it can be extended to the set
then, by conditions 1) and 2), it can be extended to the set 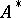 : For an arbitrary word
: For an arbitrary word  of length
of length 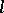 , the value
, the value 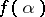 coincides with the beginning of length
coincides with the beginning of length 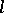 of the value
of the value 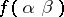 , where
, where 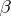 is an arbitrary superword over
is an arbitrary superword over 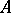 . Thus, every determined function
. Thus, every determined function 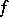 satisfies the condition:
satisfies the condition:
3) for any word 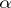 in
in 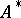 and any
and any  in
in 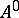 one has
one has  , where
, where 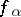 is a determined function on the set
is a determined function on the set  , uniquely determined by the word
, uniquely determined by the word 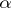 .
.
The function 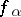 is called the remainder function for
is called the remainder function for 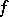 . Condition 3) implies that every determined function
. Condition 3) implies that every determined function  defines an equivalence relation
defines an equivalence relation 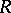 on the set
on the set 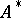 :
: 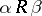 if and only if
if and only if 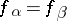 . The rank of this relation, or, which comes to the same thing, the maximum number of pairwise-distinct remainder functions, is called the weight of the determined function
. The rank of this relation, or, which comes to the same thing, the maximum number of pairwise-distinct remainder functions, is called the weight of the determined function 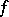 . If the weight of a determined function is finite, then the function is called a finitely-determined function. This concept can also be extended to functions of
. If the weight of a determined function is finite, then the function is called a finitely-determined function. This concept can also be extended to functions of 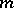 variables, where
variables, where 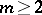 , if a collection of
, if a collection of 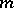 words of the same length (or superwords) over alphabets
words of the same length (or superwords) over alphabets 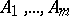 , respectively, is considered as a word (superword) over the alphabet
, respectively, is considered as a word (superword) over the alphabet 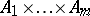 — the Cartesian product of
— the Cartesian product of 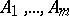 . Thus, one can consider finitely-determined functions with several outcomes, that is, whose values are sets of
. Thus, one can consider finitely-determined functions with several outcomes, that is, whose values are sets of  words or superwords over alphabets
words or superwords over alphabets 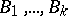 , respectively. The class of all finitely-determined functions coincides with the class of functions computable by finite automata. Hence the same means may be used to represent finitely-determined functions as are used to represent finite automata, e.g. canonical equations (see Automaton, finite; Automata, methods of specification of). This implies, in particular, that the class of finitely-determined functions with coincident alphabets
, respectively. The class of all finitely-determined functions coincides with the class of functions computable by finite automata. Hence the same means may be used to represent finitely-determined functions as are used to represent finite automata, e.g. canonical equations (see Automaton, finite; Automata, methods of specification of). This implies, in particular, that the class of finitely-determined functions with coincident alphabets 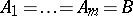 is closed under superposition. The minimal (in number of states) automaton
is closed under superposition. The minimal (in number of states) automaton 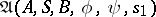 computing a finitely-determined function
computing a finitely-determined function  of weight
of weight  contains
contains  states and can be constructed as follows. Let
states and can be constructed as follows. Let  be arbitrary representatives of the equivalence classes under the relation
be arbitrary representatives of the equivalence classes under the relation 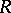 . To each class
. To each class 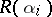 ,
, 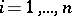 , corresponds a state
, corresponds a state 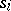 of the automaton
of the automaton 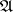 . The transition function
. The transition function 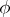 and the output function
and the output function 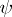 are defined by the following conditions: If
are defined by the following conditions: If 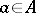 and
and 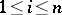 , then
, then 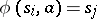 , the state
, the state 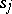 corresponds to the class
corresponds to the class 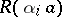 ;
; 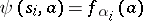 . The initial state is taken as that corresponding to the class
. The initial state is taken as that corresponding to the class 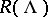 , where
, where 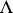 is the empty word.
is the empty word.
References
| [1] | S.C. Kleene, "Representation of events in nerve nets and finite automata" , Automata studies , 34 , Princeton Univ. Press (1956) pp. 3–41 MR0077478 |
| [2] | S.V. Yablonskii, "Introduction to discrete mathematics" , Moscow (1986) (In Russian) MR0911107 |
Comments
(Finitely-) determined functions are also called (finite) sequential machine mappings or Mealy mappings. They are a special case of gsm-mappings, for which condition 1) above is not required.
Instead of "remainder function" one also uses derivative.
A rather different notion of finite determinacy of functions occurs in differential topology. Let 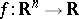 be a smooth function taking
be a smooth function taking 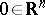 to
to 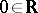 . Roughly, a function
. Roughly, a function 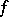 is finitely determined at
is finitely determined at  if up to local diffeomorphisms of
if up to local diffeomorphisms of 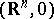 and
and 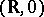 it is uniquely determined near 0 by the terms of order
it is uniquely determined near 0 by the terms of order 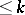 of its Taylor series at
of its Taylor series at  ; it is then said to be
; it is then said to be 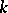 -determined. The precise notions involve germs (cf. Germ) of functions and mappings. Cf. Singularities of differentiable mappings for more details (in a more general setting) and for related notions such as stable germs of differentiable mappings, singularities of finite type, etc.
-determined. The precise notions involve germs (cf. Germ) of functions and mappings. Cf. Singularities of differentiable mappings for more details (in a more general setting) and for related notions such as stable germs of differentiable mappings, singularities of finite type, etc.
References
| [a1] | S. Ginsburg, "The mathematical theory of context-free languages" , McGraw-Hill (1965) MR0211815 Zbl 0195.02301 Zbl 0184.28401 |
| [a2] | J.E. Hopcroft, J.D. Ulman, "Introduction to automata theory, languages and computation" , Addison-Wesley (1979) MR0645539 Zbl 0426.68001 |
Finitely-determined function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Finitely-determined_function&oldid=16224