Difference between revisions of "Eikonal equation"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 20: | Line 20: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> V.M. Babich, V.S. Buldyrev, "Asymptotic methods in problems of diffraction of short waves" , Moscow (1972) (In Russian) (Translation forthcoming: Springer)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> G.B. Whitham, "Linear and nonlinear waves" , Wiley (1974) {{MR|0483954}} {{ZBL|0373.76001}} </TD></TR></table> |
| Line 28: | Line 28: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> P.R. Garabedian, "Partial differential equations" , Wiley (1964) {{MR|0162045}} {{ZBL|0124.30501}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> M.E. Taylor, "Pseudodifferential operators" , Princeton Univ. Press (1981) {{MR|0618463}} {{ZBL|0453.47026}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> M. Kline, I.W. Kay, "Electromagnetic theory and geometrical optics" , Interscience (1965) {{MR|0180094}} {{ZBL|0123.23602}} </TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> L.B. Felsen, N. Marcuvitz, "Radiation and scattering of waves" , Prentice-Hall (1973) pp. Sect. 1.7 {{MR|0471626}} {{ZBL|}} </TD></TR></table> |
Revision as of 16:57, 15 April 2012
A partial differential equation of the form
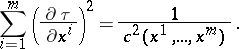 |
Here 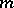 is the dimension of the space and
is the dimension of the space and  is a smooth function bounded away from zero. In applications
is a smooth function bounded away from zero. In applications  is the speed of the wave, and the surfaces
is the speed of the wave, and the surfaces 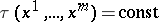 are the wave fronts. The rays (see Fermat principle) are the characteristics of the eikonal equation. This equation has a number of generalizations and analogues. In particular, one such generalization is
are the wave fronts. The rays (see Fermat principle) are the characteristics of the eikonal equation. This equation has a number of generalizations and analogues. In particular, one such generalization is
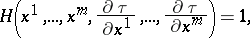 |
where the function 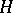 is homogeneous of degree 1 with respect to
is homogeneous of degree 1 with respect to 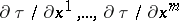 and satisfies some additional restrictions. Of considerable interest is the non-stationary analogue
and satisfies some additional restrictions. Of considerable interest is the non-stationary analogue
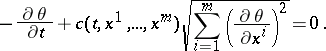 |
This is a special case of the dispersion equations occurring in the theory of wave phenomena, which have the form
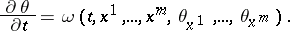 |
Here 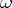 is a given function.
is a given function.
The mathematical theory of geometrical optics can be regarded as the theory of the eikonal equation. All forms of the eikonal equation are first-order partial differential equations. The solution of the eikonal equation may have singularities. Their theory is part of that of the singularities of differentiable mappings (see also Hamilton–Jacobi theory; Geometric approximation, and Ray method).
References
| [1] | V.M. Babich, V.S. Buldyrev, "Asymptotic methods in problems of diffraction of short waves" , Moscow (1972) (In Russian) (Translation forthcoming: Springer) |
| [2] | G.B. Whitham, "Linear and nonlinear waves" , Wiley (1974) MR0483954 Zbl 0373.76001 |
Comments
For a nice account of the theory of geometrical optics see [a3]; geometrical optics and pseudo-differential operator theory are treated in [a2].
References
| [a1] | P.R. Garabedian, "Partial differential equations" , Wiley (1964) MR0162045 Zbl 0124.30501 |
| [a2] | M.E. Taylor, "Pseudodifferential operators" , Princeton Univ. Press (1981) MR0618463 Zbl 0453.47026 |
| [a3] | M. Kline, I.W. Kay, "Electromagnetic theory and geometrical optics" , Interscience (1965) MR0180094 Zbl 0123.23602 |
| [a4] | L.B. Felsen, N. Marcuvitz, "Radiation and scattering of waves" , Prentice-Hall (1973) pp. Sect. 1.7 MR0471626 |
Eikonal equation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Eikonal_equation&oldid=14664