Difference between revisions of "Edge of regression"
From Encyclopedia of Mathematics
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 9: | Line 9: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> V.I. Arnol'd, S.M. [S.M. Khusein-Zade] Gusein-Zade, A.N. Varchenko, "Singularities of differentiable maps" , '''1''' , Birkhäuser (1985) (Translated from Russian) {{MR|777682}} {{ZBL|0554.58001}} </TD></TR></table> |
Revision as of 16:57, 15 April 2012
A type of singularity of differentiable mappings (cf. Singularities of differentiable mappings) of a manifold into a Euclidean space. In the simplest case of a mapping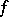 
of a surface 
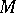into the three-dimensional Euclidean space 
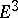an edge of regression represents a smooth curve 
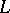in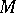 
, with smooth image 
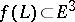, such that for any 
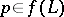the intersection of 
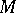with the plane 
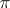through 
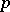and perpendicular to 
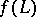is a cusp. It occurs in the pseudo-sphere.
Comments
Cf. also the edge of regression of a developable surface.
An edge of regression is also called a cuspidal edge. It is the stable caustic of type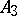 
, see [a1], p. 331.
References
| [a1] | V.I. Arnol'd, S.M. [S.M. Khusein-Zade] Gusein-Zade, A.N. Varchenko, "Singularities of differentiable maps" , 1 , Birkhäuser (1985) (Translated from Russian) MR777682 Zbl 0554.58001 |
How to Cite This Entry:
Edge of regression. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Edge_of_regression&oldid=14082
Edge of regression. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Edge_of_regression&oldid=14082
This article was adapted from an original article by M.I. Voitsekhovskii (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article