Difference between revisions of "Degree of a mapping"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 18: | Line 18: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> A. Dold, "Lectures on algebraic topology" , Springer (1980) {{MR|0606196}} {{ZBL|0434.55001}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> J.W. Milnor, "Toplogy from the differentiable viewpoint" , Univ. Virginia Press (1965)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> V.I. Arnol'd, S.M. [S.M. Khusein-Zade] Gusein-Zade, A.N. Varchenko, "Singularities of differentiable maps" , '''1''' , Birkhäuser (1985) (Translated from Russian) {{MR|777682}} {{ZBL|0554.58001}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> D. Eisenbud, H. Levine, "An algebraic formula for the degree of a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d030/d030900/d03090040.png" /> map germ" ''Ann. of Math.'' , '''106''' : 1 (1977) pp. 19–38 {{MR|467800}} {{ZBL|0398.57020}} </TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> A.H. Wallace, "Differential topology. First Steps" , Benjamin (1968) {{MR|0436148}} {{MR|0224103}} {{ZBL|0164.23805}} </TD></TR></table> |
Revision as of 16:56, 15 April 2012
degree of a continuous mapping  between connected compact manifolds of identical dimension
between connected compact manifolds of identical dimension
An integer 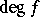 such that
such that 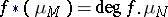 , where
, where  are the fundamental classes (cf. Fundamental class) of the manifolds
are the fundamental classes (cf. Fundamental class) of the manifolds  and
and  over the ring
over the ring  or
or 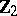 , and
, and 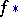 is the induced mapping. In the case of non-orientable manifolds, the degree of the mapping is uniquely defined modulo 2. If
is the induced mapping. In the case of non-orientable manifolds, the degree of the mapping is uniquely defined modulo 2. If 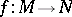 is a differentiable mapping between closed differentiable manifolds, then
is a differentiable mapping between closed differentiable manifolds, then  modulo 2 coincides with the number of inverse images of a regular value
modulo 2 coincides with the number of inverse images of a regular value 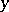 of
of 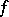 . In the case of oriented manifolds
. In the case of oriented manifolds
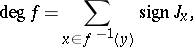 |
where  is the sign of the Jacobian of
is the sign of the Jacobian of 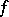 at a point
at a point  (the Browder degree).
(the Browder degree).
For a continuous mapping 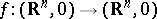 and an isolated point
and an isolated point  in the inverse image of zero, the concept of the local degree
in the inverse image of zero, the concept of the local degree 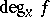 at the point
at the point  is defined:
is defined: 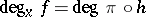 , where
, where 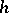 is the restriction of
is the restriction of 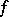 onto a small sphere
onto a small sphere
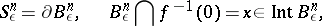 |
and  is the projection from zero onto the unit sphere. In the case of a differentiable
is the projection from zero onto the unit sphere. In the case of a differentiable  , the formula
, the formula
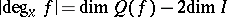 |
holds, where 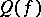 is the ring of germs (cf. Germ) of smooth functions at zero, factorized by the ideal generated by the components of
is the ring of germs (cf. Germ) of smooth functions at zero, factorized by the ideal generated by the components of 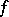 , and
, and  is the maximal ideal of the quotient ring relative to the property
is the maximal ideal of the quotient ring relative to the property 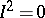 . Let
. Let 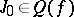 be the class of the Jacobian of the mapping
be the class of the Jacobian of the mapping 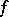 . Then for a linear form
. Then for a linear form  such that
such that 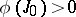 the formula
the formula 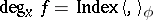 holds, where
holds, where 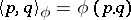 is a symmetric bilinear form on
is a symmetric bilinear form on 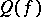 .
.
References
| [1] | A. Dold, "Lectures on algebraic topology" , Springer (1980) MR0606196 Zbl 0434.55001 |
| [2] | J.W. Milnor, "Toplogy from the differentiable viewpoint" , Univ. Virginia Press (1965) |
| [3] | V.I. Arnol'd, S.M. [S.M. Khusein-Zade] Gusein-Zade, A.N. Varchenko, "Singularities of differentiable maps" , 1 , Birkhäuser (1985) (Translated from Russian) MR777682 Zbl 0554.58001 |
| [4] | D. Eisenbud, H. Levine, "An algebraic formula for the degree of a 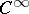 map germ" Ann. of Math. , 106 : 1 (1977) pp. 19–38 MR467800 Zbl 0398.57020 map germ" Ann. of Math. , 106 : 1 (1977) pp. 19–38 MR467800 Zbl 0398.57020 |
| [5] | A.H. Wallace, "Differential topology. First Steps" , Benjamin (1968) MR0436148 MR0224103 Zbl 0164.23805 |
Degree of a mapping. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Degree_of_a_mapping&oldid=14689