Difference between revisions of "Cluster set"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 9: | Line 9: | ||
If the entire domain <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266017.png" /> is taken for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266018.png" />, one obtains the full cluster set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266019.png" />; if the inclusion <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266020.png" /> is strict, the corresponding set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266021.png" /> is sometimes called a partial cluster set. A full cluster set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266022.png" /> is closed; if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266023.png" /> is continuous on a set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266024.png" /> that is locally connected at <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266025.png" />, then the cluster set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266026.png" /> is either degenerate, i.e. consists of a single point, or is a non-degenerate continuum. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266027.png" /> coincides with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266028.png" />, then it is called a total cluster set. A number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266029.png" /> belongs to the set of recurrent values <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266030.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266031.png" /> at <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266032.png" /> with respect to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266033.png" /> if there is a sequence <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266034.png" /> of points <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266035.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266036.png" /> <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266037.png" />, such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266038.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266039.png" />. One always has <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266040.png" />. If for some <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266041.png" /> there is a path <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266042.png" />: <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266043.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266044.png" />, in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266045.png" /> ending at a point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266046.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266047.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266048.png" />, and such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266049.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266050.png" /> is called an [[Asymptotic value|asymptotic value]] of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266051.png" /> at <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266052.png" /> (along <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266053.png" />). The asymptotic set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266054.png" /> is the set of all asymptotic values of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266055.png" /> at <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266056.png" />. | If the entire domain <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266017.png" /> is taken for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266018.png" />, one obtains the full cluster set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266019.png" />; if the inclusion <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266020.png" /> is strict, the corresponding set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266021.png" /> is sometimes called a partial cluster set. A full cluster set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266022.png" /> is closed; if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266023.png" /> is continuous on a set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266024.png" /> that is locally connected at <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266025.png" />, then the cluster set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266026.png" /> is either degenerate, i.e. consists of a single point, or is a non-degenerate continuum. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266027.png" /> coincides with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266028.png" />, then it is called a total cluster set. A number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266029.png" /> belongs to the set of recurrent values <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266030.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266031.png" /> at <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266032.png" /> with respect to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266033.png" /> if there is a sequence <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266034.png" /> of points <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266035.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266036.png" /> <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266037.png" />, such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266038.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266039.png" />. One always has <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266040.png" />. If for some <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266041.png" /> there is a path <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266042.png" />: <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266043.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266044.png" />, in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266045.png" /> ending at a point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266046.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266047.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266048.png" />, and such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266049.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266050.png" /> is called an [[Asymptotic value|asymptotic value]] of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266051.png" /> at <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266052.png" /> (along <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266053.png" />). The asymptotic set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266054.png" /> is the set of all asymptotic values of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266055.png" /> at <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266056.png" />. | ||
| − | The notion of a cluster set was clearly formulated for the first time by P. Painlevé in 1895 (he called it the | + | The notion of a cluster set was clearly formulated for the first time by P. Painlevé in 1895 (he called it the "region of indeterminacy" , cf. [[#References|[1]]]) in connection with studying an analytic function near one of its singular points and with classifying singularities of such functions. At that time one basically studied three, geometrically most simple, cases in the theory of cluster sets: a) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266057.png" /> is an isolated point of the boundary <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266058.png" /> or an interior point of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266059.png" />; b) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266060.png" /> is the unit disc or, in general, a Jordan domain, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266061.png" /> is a point on the boundary <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266062.png" />; and c) the boundary <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266063.png" /> is an everywhere-discontinuous compactum in the plane (i.e. a totally-disconnected compact set) and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266064.png" />. A number of classical results in complex function theory have a formulation in terms of cluster sets. E.g., the [[Sokhotskii theorem|Sokhotskii theorem]], in a somewhat stronger form, states: If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266065.png" /> is an isolated point of an everywhere-discontinuous compactum <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266066.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266067.png" /> is a meromorphic function on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266068.png" />, then the cluster set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266069.png" /> is either degenerate or total. The [[Picard theorem|Picard theorem]], supplementing it, states that if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266070.png" /> is total, i.e. if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266071.png" /> is an essential singular point, then the set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266072.png" /> contains at most two different values. Also, in this case |
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266073.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266073.png" /></td> </tr></table> | ||
| Line 15: | Line 15: | ||
(the [[Iversen theorem|Iversen theorem]]). | (the [[Iversen theorem|Iversen theorem]]). | ||
| − | The main result related to the theory of the behaviour of meromorphic functions near | + | The main result related to the theory of the behaviour of meromorphic functions near "thin" boundaries (the Painlevé theory) is (cf. [[#References|[1]]], [[#References|[2]]]): If a set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266074.png" /> has linear Hausdorff measure zero, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266075.png" />, and the function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266076.png" /> is meromorphic in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266077.png" />, then for every point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266078.png" /> the cluster set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266079.png" /> is either degenerate or total; moreover, in the first case <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266080.png" /> is also meromorphic at <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266081.png" />. Thus, a point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266082.png" /> for which the cluster set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266083.png" /> is degenerate is a removable singular point of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266084.png" />; the study of removable sets of various function classes can be regarded as a branch of the theory of cluster sets. |
Golubev's theorem is an important strengthening of the theorem of Picard: If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266085.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266086.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266087.png" /> is meromorphic in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266088.png" />, then the set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266089.png" /> has [[Analytic capacity|analytic capacity]] zero at every essential singular point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266090.png" /> (hence its plane measure <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266091.png" />). | Golubev's theorem is an important strengthening of the theorem of Picard: If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266085.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266086.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266087.png" /> is meromorphic in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266088.png" />, then the set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266089.png" /> has [[Analytic capacity|analytic capacity]] zero at every essential singular point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266090.png" /> (hence its plane measure <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c02266091.png" />). | ||
| Line 49: | Line 49: | ||
is open (for any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c022660176.png" />), and all values <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c022660177.png" />, with possibly two exceptions, belong to the set of recurrent values <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c022660178.png" />. Moreover, every exceptional value (if existing) is an asymptotic value of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c022660179.png" /> at <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c022660180.png" />. | is open (for any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c022660176.png" />), and all values <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c022660177.png" />, with possibly two exceptions, belong to the set of recurrent values <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c022660178.png" />. Moreover, every exceptional value (if existing) is an asymptotic value of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c022660179.png" /> at <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c022660180.png" />. | ||
| − | The research of Iversen and Gross obtained a further development in the work of A. Beurling, W. Seidel (who in 1932 also introduced the term | + | The research of Iversen and Gross obtained a further development in the work of A. Beurling, W. Seidel (who in 1932 also introduced the term "cluster set" ) and others (cf. [[#References|[5]]]–[[#References|[9]]]). They basically considered the case when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c022660181.png" /> belongs to a "small" set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c022660182.png" /> on the boundary <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c022660183.png" />, having zero linear measure or zero capacity, and studied the cluster set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c022660184.png" />, defined analogously to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c022660185.png" />. Methods of potential theory are also used in these studies. |
The most recent results in this direction are stated below for the case of the disc <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c022660186.png" />. Suppose a set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c022660187.png" /> on an arc <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c022660188.png" /> of the boundary <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c022660189.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c022660190.png" /> having <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c022660191.png" /> is fixed, and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c022660192.png" />. To every point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c022660193.png" /> one assigns a Jordan arc <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c022660194.png" /> ending at <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c022660195.png" />. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c022660196.png" /> be the closure of the union <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c022660197.png" /> over all points | The most recent results in this direction are stated below for the case of the disc <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c022660186.png" />. Suppose a set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c022660187.png" /> on an arc <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c022660188.png" /> of the boundary <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c022660189.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c022660190.png" /> having <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c022660191.png" /> is fixed, and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c022660192.png" />. To every point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c022660193.png" /> one assigns a Jordan arc <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c022660194.png" /> ending at <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c022660195.png" />. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c022660196.png" /> be the closure of the union <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c022660197.png" /> over all points | ||
| Line 118: | Line 118: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> P. Painlevé, "Leçons sur la théorie analytique des équations différentielles, professées à Stockholm (1895)" , Paris (1897)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> B. Zoretti, "Leçons sur la prolongement analytique" , Gauthier-Villars (1911)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> V.V. Golubev, "Univalent analytic functions. Automorphic functions" , Moscow (1961) (In Russian)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> I.I. [I.I. Privalov] Priwalow, "Randeigenschaften analytischer Funktionen" , Deutsch. Verlag Wissenschaft. (1956) (Translated from Russian) {{MR|0083565}} {{ZBL|}} </TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> K. Noshiro, "Cluster sets" , Springer (1960) {{MR|0133464}} {{ZBL|0090.28801}} </TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> E.F. Collingwood, A.J. Lohwater, "The theory of cluster sets" , Cambridge Univ. Press (1966) pp. Chapt. 9 {{MR|0231999}} {{ZBL|0149.03003}} </TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> G.R. MacLane, "Asymptotic values of holomorphic functions" , ''Rice Univ. Studies, Math. Monographs'' , '''49''' : 1 , Rice Univ. , Houston (1963)</TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> A.I. Markushevich, G.Ts. Tumarkin, S.Ya. Khavinson, , ''Studies on comtemporary problems in the theory of functions of a complex variable'' , Moscow (1961) pp. 100–110 (In Russian)</TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> A. Lohwater, "The boundary behaviour of analytic functions" ''Itogi Nauk. Mat. Anal.'' , '''10''' (1973) pp. 99–259 (In Russian)</TD></TR><TR><TD valign="top">[10]</TD> <TD valign="top"> E.P. Dolzhenko, "Boundary properties of arbitrary functions" ''Izv. Akad. Nauk SSSR Ser. Mat.'' , '''31''' : 1 (1967) pp. 3–14 (In Russian)</TD></TR><TR><TD valign="top">[11]</TD> <TD valign="top"> E.P. Dolzhenko, "The metric properties of singular sets of holomorphic functions of several variables" ''Ann. of Math.'' , '''2''' (1976) pp. 191–201 (In Russian) (English summary)</TD></TR><TR><TD valign="top">[12]</TD> <TD valign="top"> V.I. Gavrilov, "Behavior of holomorphic functions along a chord in the unit disk" ''Soviet Math. Dokl.'' , '''15''' : 3 (1974) pp. 725–728 ''Dokl. Akad. Nauk SSSR'' , '''216''' : 1 (1974) pp. 21–23</TD></TR><TR><TD valign="top">[13]</TD> <TD valign="top"> A.N. Kanatnikov, V.I. Gavrilov, "Characterization of the set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c022660332.png" /> for meromorphic functions" ''Soviet Math. Dokl.'' , '''18''' : 2 (1977) pp. 270–272 ''Dokl. Akad. Nauk SSSR'' , '''233''' : 1 (1977) pp. 15–17 {{MR|437770}} {{ZBL|0377.30022}} {{ZBL|0373.30029}} </TD></TR><TR><TD valign="top">[14]</TD> <TD valign="top"> A.N. Kanatnikov, "A converse to Meier's theorem on meromorphic functions" ''Soviet Math. Dokl.'' , '''19''' : 1 (1978) pp. 162–165 ''Dokl. Akad. Nauk SSSR'' , '''238''' : 5 (1978) pp. 1043–1046 {{MR|477055}} {{ZBL|}} </TD></TR><TR><TD valign="top">[15]</TD> <TD valign="top"> W. Rudin, "Function theory in polydiscs" , Benjamin (1969) {{MR|0255841}} {{ZBL|0177.34101}} </TD></TR><TR><TD valign="top">[16]</TD> <TD valign="top"> G.M. Khenkin, E.M. Chirka, "Boundary properties of holomorphic functions of several complex variables" ''J. Soviet Math.'' , '''5''' (1976) pp. 612–687 ''Itogi Nauk. i Tekhn. Sovrem. Probl. Mat.'' , '''4''' (1975) pp. 13–142</TD></TR><TR><TD valign="top">[17]</TD> <TD valign="top"> W. Rudin, "Function theory in the unit ball in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022660/c022660333.png" />" , Springer (1980) {{MR|601594}} {{ZBL|0495.32001}} </TD></TR></table> |
Revision as of 16:56, 15 April 2012
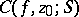 of a function
of a function 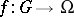 , defined on a domain
, defined on a domain 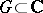 with values in the Riemann sphere
with values in the Riemann sphere  , at a point
, at a point 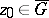 with respect to a set
with respect to a set  ,
, 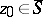
The set of values 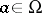 for which there exists a sequence of points
for which there exists a sequence of points 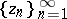 ,
, 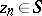 ,
, 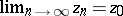 , such that
, such that
 |
Every number 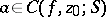 is called a cluster value of
is called a cluster value of 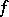 at
at  with respect to
with respect to 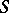 . The theory of cluster sets is a branch of function theory in which boundary properties of functions are studied in terms of topological and metric properties of various cluster sets.
. The theory of cluster sets is a branch of function theory in which boundary properties of functions are studied in terms of topological and metric properties of various cluster sets.
If the entire domain 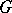 is taken for
is taken for 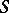 , one obtains the full cluster set
, one obtains the full cluster set 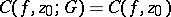 ; if the inclusion
; if the inclusion 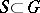 is strict, the corresponding set
is strict, the corresponding set 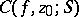 is sometimes called a partial cluster set. A full cluster set
is sometimes called a partial cluster set. A full cluster set  is closed; if
is closed; if 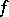 is continuous on a set
is continuous on a set 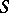 that is locally connected at
that is locally connected at 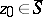 , then the cluster set
, then the cluster set 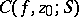 is either degenerate, i.e. consists of a single point, or is a non-degenerate continuum. If
is either degenerate, i.e. consists of a single point, or is a non-degenerate continuum. If 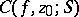 coincides with
coincides with  , then it is called a total cluster set. A number
, then it is called a total cluster set. A number  belongs to the set of recurrent values
belongs to the set of recurrent values 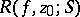 of
of 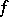 at
at 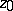 with respect to
with respect to 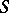 if there is a sequence
if there is a sequence 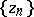 of points
of points 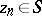 ,
, 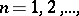
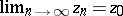 , such that
, such that 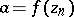 ,
, 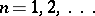 . One always has
. One always has  . If for some
. If for some 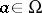 there is a path
there is a path 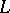 :
: 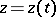 ,
, 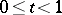 , in
, in  ending at a point
ending at a point 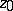 ,
, 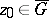 ,
, 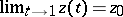 , and such that
, and such that 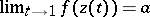 , then
, then  is called an asymptotic value of
is called an asymptotic value of 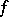 at
at 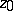 (along
(along 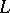 ). The asymptotic set
). The asymptotic set 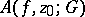 is the set of all asymptotic values of
is the set of all asymptotic values of 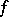 at
at 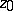 .
.
The notion of a cluster set was clearly formulated for the first time by P. Painlevé in 1895 (he called it the "region of indeterminacy" , cf. [1]) in connection with studying an analytic function near one of its singular points and with classifying singularities of such functions. At that time one basically studied three, geometrically most simple, cases in the theory of cluster sets: a) 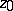 is an isolated point of the boundary
is an isolated point of the boundary 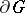 or an interior point of
or an interior point of 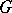 ; b)
; b) 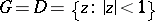 is the unit disc or, in general, a Jordan domain, and
is the unit disc or, in general, a Jordan domain, and 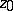 is a point on the boundary
is a point on the boundary 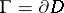 ; and c) the boundary
; and c) the boundary 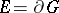 is an everywhere-discontinuous compactum in the plane (i.e. a totally-disconnected compact set) and
is an everywhere-discontinuous compactum in the plane (i.e. a totally-disconnected compact set) and 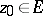 . A number of classical results in complex function theory have a formulation in terms of cluster sets. E.g., the Sokhotskii theorem, in a somewhat stronger form, states: If
. A number of classical results in complex function theory have a formulation in terms of cluster sets. E.g., the Sokhotskii theorem, in a somewhat stronger form, states: If 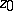 is an isolated point of an everywhere-discontinuous compactum
is an isolated point of an everywhere-discontinuous compactum 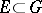 and
and 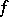 is a meromorphic function on
is a meromorphic function on 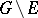 , then the cluster set
, then the cluster set 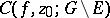 is either degenerate or total. The Picard theorem, supplementing it, states that if
is either degenerate or total. The Picard theorem, supplementing it, states that if 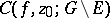 is total, i.e. if
is total, i.e. if 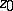 is an essential singular point, then the set
is an essential singular point, then the set 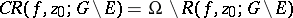 contains at most two different values. Also, in this case
contains at most two different values. Also, in this case
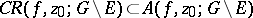 |
(the Iversen theorem).
The main result related to the theory of the behaviour of meromorphic functions near "thin" boundaries (the Painlevé theory) is (cf. [1], [2]): If a set 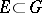 has linear Hausdorff measure zero,
has linear Hausdorff measure zero, 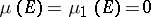 , and the function
, and the function 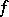 is meromorphic in
is meromorphic in 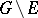 , then for every point
, then for every point 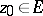 the cluster set
the cluster set  is either degenerate or total; moreover, in the first case
is either degenerate or total; moreover, in the first case 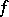 is also meromorphic at
is also meromorphic at 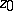 . Thus, a point
. Thus, a point 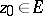 for which the cluster set
for which the cluster set 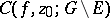 is degenerate is a removable singular point of
is degenerate is a removable singular point of 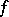 ; the study of removable sets of various function classes can be regarded as a branch of the theory of cluster sets.
; the study of removable sets of various function classes can be regarded as a branch of the theory of cluster sets.
Golubev's theorem is an important strengthening of the theorem of Picard: If 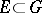 ,
, 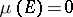 and
and 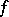 is meromorphic in
is meromorphic in 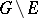 , then the set
, then the set 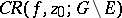 has analytic capacity zero at every essential singular point
has analytic capacity zero at every essential singular point 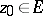 (hence its plane measure
(hence its plane measure 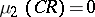 ).
).
The work of P. Fatou (1906) on boundary values of functions 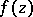 holomorphic in the unit disc
holomorphic in the unit disc 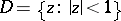 was the starting point for the theory of cluster sets in the case of continuous boundaries. If such a function
was the starting point for the theory of cluster sets in the case of continuous boundaries. If such a function 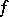 is bounded in
is bounded in 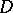 , then almost-everywhere (in the sense of the Lebesgue measure) on the circle
, then almost-everywhere (in the sense of the Lebesgue measure) on the circle 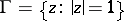 it has radial and angular (non-tangential) boundary values (Fatou's theorem). Let
it has radial and angular (non-tangential) boundary values (Fatou's theorem). Let 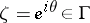 be an arbitrary point; denote by
be an arbitrary point; denote by 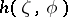 the chord of
the chord of 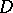 ending at
ending at 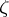 and forming with the radius at
and forming with the radius at 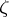 an angle
an angle 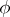 ,
,  . Let
. Let 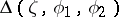 be the angular domain with vertex
be the angular domain with vertex 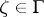 , consisting of those points of
, consisting of those points of 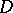 lying between the chords
lying between the chords
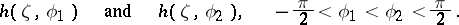 |
A point 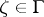 is called a Fatou point, and belongs to the set
is called a Fatou point, and belongs to the set 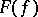 , if the union
, if the union
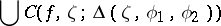 |
over all angular domains 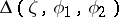 consists of a single value
consists of a single value 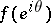 , which is called the angular boundary value of
, which is called the angular boundary value of 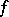 at
at 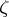 . Another formulation of Fatou's theorem: For a bounded holomorphic function
. Another formulation of Fatou's theorem: For a bounded holomorphic function 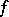 in
in 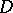 the decomposition
the decomposition 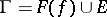 ,
, 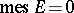 , holds. This result is supplemented by the F. and M. Riesz uniqueness theorem (1916): If
, holds. This result is supplemented by the F. and M. Riesz uniqueness theorem (1916): If 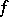 is holomorphic and bounded in
is holomorphic and bounded in 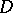 and if on some set
and if on some set 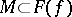 ,
, 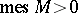 , it has angular boundary values
, it has angular boundary values 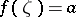 ,
, 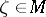 , then
, then 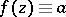 . This statement was proved, independently, by N.N. Luzin and I.I. Privalov (1919), who obtained an essential generalization of it to the case of arbitrary meromorphic functions. In the same year they published a boundary uniqueness theorem for the case of radial boundary values: If a function
. This statement was proved, independently, by N.N. Luzin and I.I. Privalov (1919), who obtained an essential generalization of it to the case of arbitrary meromorphic functions. In the same year they published a boundary uniqueness theorem for the case of radial boundary values: If a function 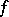 , holomorphic in
, holomorphic in 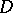 , has the same radial boundary value
, has the same radial boundary value 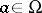 on a set
on a set 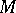 of the second category and metrically dense on some arc
of the second category and metrically dense on some arc 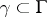 , i.e. if
, i.e. if 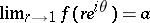 ,
, 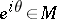 , then
, then 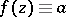 .
.
Privalov, in 1936, noted that the statement  remains true also when the values
remains true also when the values 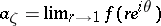 are not necessarily equal at the points
are not necessarily equal at the points 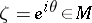 , but belong to a set of (logarithmic) capacity zero. The basic idea and the elements of the proof of the Luzin–Privalov theorem are applicable in the general case of continuous mappings
, but belong to a set of (logarithmic) capacity zero. The basic idea and the elements of the proof of the Luzin–Privalov theorem are applicable in the general case of continuous mappings 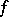 of
of  , which was subsequently used in many papers.
, which was subsequently used in many papers.
A point 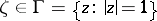 is called a Plessner point, and belongs to the set
is called a Plessner point, and belongs to the set 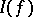 , if the intersection
, if the intersection
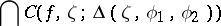 |
over all angular domains 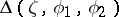 with vertex
with vertex 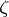 coincides with
coincides with  . A.I. Plessner proved (1927) that for a meromorphic function
. A.I. Plessner proved (1927) that for a meromorphic function 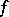 in
in 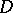 almost-all points of the boundary
almost-all points of the boundary 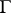 belong either to
belong either to 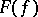 or to
or to  , i.e.
, i.e. 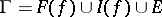 ,
, 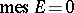 . A point
. A point 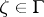 is called a Meier point, and belongs to
is called a Meier point, and belongs to 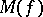 , if
, if 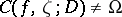 and if the intersection of the chordal cluster sets,
and if the intersection of the chordal cluster sets, 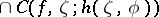 , over all chords drawn at
, over all chords drawn at 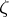 , coincides with
, coincides with  . K. Meier established (1961) the following analogue of Plessner's theorem in terms of Baire categories: If
. K. Meier established (1961) the following analogue of Plessner's theorem in terms of Baire categories: If 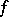 is meromorphic in
is meromorphic in 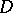 , then all points of the boundary
, then all points of the boundary 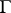 , with the possible exception of a set
, with the possible exception of a set 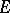 of the first category, belong to the union
of the first category, belong to the union 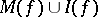 . A more precise statement of Meier's theorem has been obtained, in which
. A more precise statement of Meier's theorem has been obtained, in which 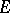 is a set of the first category and of type
is a set of the first category and of type 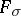 (cf. [12]–[14], in which generalizations of Plessner's and Meier's theorems have been obtained, and in which a converse of Meier's theorem and a characterization of
(cf. [12]–[14], in which generalizations of Plessner's and Meier's theorems have been obtained, and in which a converse of Meier's theorem and a characterization of 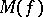 have been given).
have been given).
The work of Fatou served as an original source for the development of fundamental research on boundary properties of analytic functions. The studies of F. and M. Riesz, Luzin, Privalov, R. Nevanlinna, Plessner, V.I. Smirnov, and others were conducted independently of the ideas of Painlevé, and the use of methods related to measure and integration theory, including the notion of Baire categories, is characteristic for them (cf. [4]–[9]).
The basic objects of study for F. Iversen and W. Gross were meromorphic functions 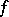 in domains
in domains 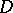 with a Jordan boundary
with a Jordan boundary 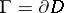 . At an arbitrary point
. At an arbitrary point 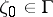 , the boundary cluster set
, the boundary cluster set 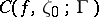 is defined as follows: If
is defined as follows: If 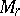 denotes the closure of the union
denotes the closure of the union 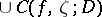 over all points
over all points
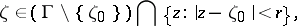 |
then 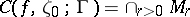 . One of the main theorems obtained, independently, by them asserts that, under the conditions stated, the set
. One of the main theorems obtained, independently, by them asserts that, under the conditions stated, the set
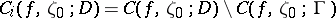 |
is open (for any 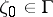 ), and all values
), and all values 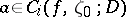 , with possibly two exceptions, belong to the set of recurrent values
, with possibly two exceptions, belong to the set of recurrent values 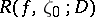 . Moreover, every exceptional value (if existing) is an asymptotic value of
. Moreover, every exceptional value (if existing) is an asymptotic value of 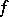 at
at 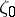 .
.
The research of Iversen and Gross obtained a further development in the work of A. Beurling, W. Seidel (who in 1932 also introduced the term "cluster set" ) and others (cf. [5]–[9]). They basically considered the case when 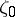 belongs to a "small" set
belongs to a "small" set 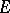 on the boundary
on the boundary 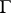 , having zero linear measure or zero capacity, and studied the cluster set
, having zero linear measure or zero capacity, and studied the cluster set 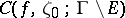 , defined analogously to
, defined analogously to 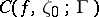 . Methods of potential theory are also used in these studies.
. Methods of potential theory are also used in these studies.
The most recent results in this direction are stated below for the case of the disc 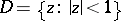 . Suppose a set
. Suppose a set 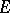 on an arc
on an arc 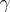 of the boundary
of the boundary 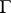 of
of 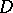 having
having 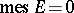 is fixed, and let
is fixed, and let 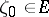 . To every point
. To every point 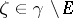 one assigns a Jordan arc
one assigns a Jordan arc 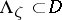 ending at
ending at 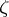 . Let
. Let 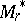 be the closure of the union
be the closure of the union 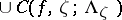 over all points
over all points
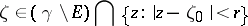 |
and suppose
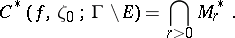 |
Then the set
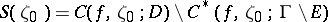 |
is open, the set 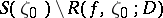 has capacity zero, and every value
has capacity zero, and every value 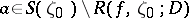 is an asymptotic value of
is an asymptotic value of 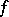 either at
either at 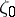 or at every point of some sequence
or at every point of some sequence 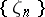 ,
, 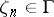 ,
, 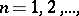
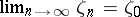 . If
. If 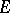 has capacity zero, then for every connected component
has capacity zero, then for every connected component 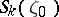 ,
, 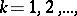 of
of 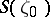 the set
the set 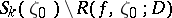 consists of at most two distinct values.
consists of at most two distinct values.
Lindelöf's theorem has been proved using normal families (cf. Normal family): If a holomorphic function 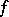 is bounded in
is bounded in 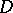 and has asymptotic value
and has asymptotic value  at
at 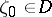 , then it has at this point
, then it has at this point  as angular boundary value. Normality of a family
as angular boundary value. Normality of a family 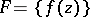 of meromorphic functions
of meromorphic functions 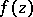 in a domain
in a domain 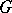 can be characterized in terms of the so-called spherical derivative
can be characterized in terms of the so-called spherical derivative
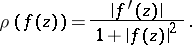 |
To be precise, 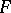 is a normal family if and only if the spherical derivatives
is a normal family if and only if the spherical derivatives 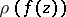 ,
, 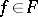 , are uniformly bounded inside
, are uniformly bounded inside 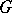 , i.e. if for every compactum
, i.e. if for every compactum 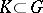 there is a constant
there is a constant  such that
such that
 |
However, the most important occurrence of normal families in the theory of cluster sets is in the notion of a normal function. A function 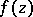 , meromorphic in a simply-connected domain
, meromorphic in a simply-connected domain 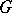 , is called a normal function in
, is called a normal function in 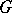 if the family
if the family 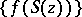 , where
, where 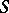 runs through the family of all conformal automorphisms of
runs through the family of all conformal automorphisms of 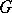 , is normal;
, is normal; 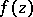 is normal in a multiply-connected domain
is normal in a multiply-connected domain 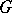 if it is normal on the universal covering surface of
if it is normal on the universal covering surface of 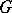 . A function
. A function 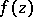 , meromorphic in
, meromorphic in 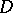 , is normal if and only if there is a constant
, is normal if and only if there is a constant 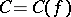 ,
, 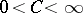 , such that
, such that
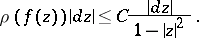 |
Here, the left-hand side is the line element in the so-called chordal metric on the Riemann sphere  for the mapping
for the mapping 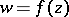 , while the expression
, while the expression 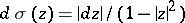 is the hyperbolic metric of
is the hyperbolic metric of 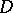 . Bounded holomorphic functions and meromorphic functions not taking three distinct values are normal, and certain properties of functions of the classes indicated carry over to arbitrary normal functions. E.g., the conclusion of Lindelöf's theorem holds for arbitrary normal functions. The class of all normal meromorphic functions in
. Bounded holomorphic functions and meromorphic functions not taking three distinct values are normal, and certain properties of functions of the classes indicated carry over to arbitrary normal functions. E.g., the conclusion of Lindelöf's theorem holds for arbitrary normal functions. The class of all normal meromorphic functions in 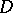 has some resemblance to the class of functions of bounded characteristic (cf. Function of bounded characteristic). There are, however, essential differences. E.g., there exist normal meromorphic functions without asymptotic values, hence without radial boundary values, a fact which cannot hold for functions of bounded characteristic. G.R. MacLane [7], [9] conducted important studies on asymptotic values. MacLane's theory allows one to obtain new proofs of already known properties of normal functions. E.g., the set of points
has some resemblance to the class of functions of bounded characteristic (cf. Function of bounded characteristic). There are, however, essential differences. E.g., there exist normal meromorphic functions without asymptotic values, hence without radial boundary values, a fact which cannot hold for functions of bounded characteristic. G.R. MacLane [7], [9] conducted important studies on asymptotic values. MacLane's theory allows one to obtain new proofs of already known properties of normal functions. E.g., the set of points 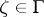 at which a normal holomorphic function
at which a normal holomorphic function 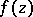 has asymptotic values, hence angular boundary values, is dense on
has asymptotic values, hence angular boundary values, is dense on 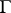 .
.
The value distribution of meromorphic functions is closely connected with the notion of normality. A sequence  of points
of points 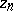 in
in 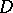 with
with 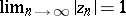 is called a
is called a 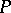 -sequence for a meromorphic function
-sequence for a meromorphic function 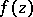 in
in 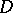 if for every infinite subsequence
if for every infinite subsequence 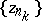 and every
and every 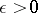 the set
the set
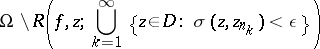 |
contains at most two values. It has been proved that 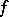 has at least one
has at least one  -sequence if and only if
-sequence if and only if
 |
Thus, the value distribution of the meromorphic function 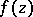 is related to the structure of the cluster set of the continuous function
is related to the structure of the cluster set of the continuous function  .
.
Substantial progress has been made on the theory of cluster sets of general mappings 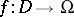 ,
, 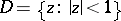 . Already in 1955 the ambiguous point theorem was proved: Let
. Already in 1955 the ambiguous point theorem was proved: Let 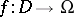 be an arbitrary mapping; then the points
be an arbitrary mapping; then the points 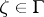 at which one can draw two continuous curves
at which one can draw two continuous curves  and
and 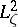 such that
such that
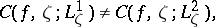 |
form a set that is at most countable. Collingwood's maximality theorem: Let 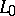 be an arbitrary continuum in
be an arbitrary continuum in 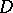 such that
such that 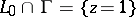 , let
, let  be the continuum obtained from
be the continuum obtained from  by rotation over
by rotation over 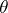 around the coordinate origin and let
around the coordinate origin and let 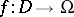 be an arbitrary mapping; then the points
be an arbitrary mapping; then the points 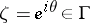 at which
at which
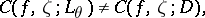 |
form a set of the first category on 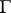 . A point
. A point 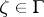 is said to belong to the set
is said to belong to the set  if the cluster set
if the cluster set 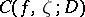 coincides with the intersection
coincides with the intersection
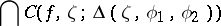 |
over all angular domains with vertex 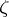 . It has been proved [10] that
. It has been proved [10] that
 |
for an arbitrary mapping 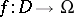 , where
, where 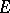 is a set of the first category of type
is a set of the first category of type 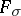 . Conversely, for an arbitrary set
. Conversely, for an arbitrary set 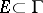 of the first category and of type
of the first category and of type 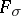 there exists a function
there exists a function 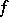 , holomorphic and bounded in
, holomorphic and bounded in 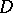 , for which
, for which 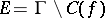 . The set
. The set 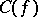 is a subset of the set
is a subset of the set 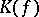 of all
of all 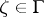 at which
at which
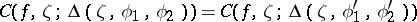 |
for any two angular domains 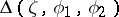 and
and 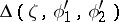 . Let
. Let 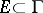 and
and 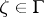 . For a given
. For a given 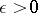 let
let 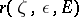 denote the length of the largest open arc on
denote the length of the largest open arc on 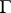 contained in the
contained in the  -neighbourhood
-neighbourhood 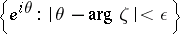 of
of  and not having points in common with
and not having points in common with 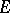 ; if such an arc does not exist,
; if such an arc does not exist, 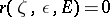 . A set
. A set 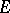 is called porous on
is called porous on 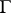 if for any point
if for any point  ,
,
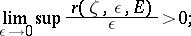 |
a 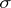 -porous set is a union of at most countably many porous sets. Every
-porous set is a union of at most countably many porous sets. Every  -porous set is of the first category and has linear measure zero. The equality
-porous set is of the first category and has linear measure zero. The equality 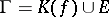 is valid for any mapping
is valid for any mapping 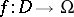 , where
, where  is a
is a 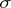 -porous set of type
-porous set of type 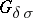 . Conversely, for an arbitrary
. Conversely, for an arbitrary 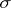 -porous set
-porous set 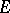 there exists a function
there exists a function 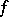 , holomorphic and bounded in
, holomorphic and bounded in 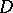 , such that
, such that 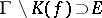 .
.
About the theory of cluster sets of functions of several complex variables see, e.g., [15]–[17].
References
| [1] | P. Painlevé, "Leçons sur la théorie analytique des équations différentielles, professées à Stockholm (1895)" , Paris (1897) |
| [2] | B. Zoretti, "Leçons sur la prolongement analytique" , Gauthier-Villars (1911) |
| [3] | V.V. Golubev, "Univalent analytic functions. Automorphic functions" , Moscow (1961) (In Russian) |
| [4] | I.I. [I.I. Privalov] Priwalow, "Randeigenschaften analytischer Funktionen" , Deutsch. Verlag Wissenschaft. (1956) (Translated from Russian) MR0083565 |
| [5] | K. Noshiro, "Cluster sets" , Springer (1960) MR0133464 Zbl 0090.28801 |
| [6] | E.F. Collingwood, A.J. Lohwater, "The theory of cluster sets" , Cambridge Univ. Press (1966) pp. Chapt. 9 MR0231999 Zbl 0149.03003 |
| [7] | G.R. MacLane, "Asymptotic values of holomorphic functions" , Rice Univ. Studies, Math. Monographs , 49 : 1 , Rice Univ. , Houston (1963) |
| [8] | A.I. Markushevich, G.Ts. Tumarkin, S.Ya. Khavinson, , Studies on comtemporary problems in the theory of functions of a complex variable , Moscow (1961) pp. 100–110 (In Russian) |
| [9] | A. Lohwater, "The boundary behaviour of analytic functions" Itogi Nauk. Mat. Anal. , 10 (1973) pp. 99–259 (In Russian) |
| [10] | E.P. Dolzhenko, "Boundary properties of arbitrary functions" Izv. Akad. Nauk SSSR Ser. Mat. , 31 : 1 (1967) pp. 3–14 (In Russian) |
| [11] | E.P. Dolzhenko, "The metric properties of singular sets of holomorphic functions of several variables" Ann. of Math. , 2 (1976) pp. 191–201 (In Russian) (English summary) |
| [12] | V.I. Gavrilov, "Behavior of holomorphic functions along a chord in the unit disk" Soviet Math. Dokl. , 15 : 3 (1974) pp. 725–728 Dokl. Akad. Nauk SSSR , 216 : 1 (1974) pp. 21–23 |
| [13] | A.N. Kanatnikov, V.I. Gavrilov, "Characterization of the set 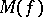 for meromorphic functions" Soviet Math. Dokl. , 18 : 2 (1977) pp. 270–272 Dokl. Akad. Nauk SSSR , 233 : 1 (1977) pp. 15–17 MR437770 Zbl 0377.30022 Zbl 0373.30029 for meromorphic functions" Soviet Math. Dokl. , 18 : 2 (1977) pp. 270–272 Dokl. Akad. Nauk SSSR , 233 : 1 (1977) pp. 15–17 MR437770 Zbl 0377.30022 Zbl 0373.30029 |
| [14] | A.N. Kanatnikov, "A converse to Meier's theorem on meromorphic functions" Soviet Math. Dokl. , 19 : 1 (1978) pp. 162–165 Dokl. Akad. Nauk SSSR , 238 : 5 (1978) pp. 1043–1046 MR477055 |
| [15] | W. Rudin, "Function theory in polydiscs" , Benjamin (1969) MR0255841 Zbl 0177.34101 |
| [16] | G.M. Khenkin, E.M. Chirka, "Boundary properties of holomorphic functions of several complex variables" J. Soviet Math. , 5 (1976) pp. 612–687 Itogi Nauk. i Tekhn. Sovrem. Probl. Mat. , 4 (1975) pp. 13–142 |
| [17] | W. Rudin, "Function theory in the unit ball in 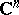 " , Springer (1980) MR601594 Zbl 0495.32001 " , Springer (1980) MR601594 Zbl 0495.32001 |
Comments
For the notions of linear Hausdorff measure and plane measure cf. Hausdorff measure; for the chordal metric (also called spherical metric) cf. Extended complex plane.
Cluster set. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cluster_set&oldid=16145