Difference between revisions of "Witt decomposition"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 34: | Line 34: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> N. Bourbaki, "Algebra" , ''Elements of mathematics'' , '''1''' , Addison-Wesley (1974) pp. Chapts. 1–2 (Translated from French) {{MR|0354207}} {{ZBL|0281.00006}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> S. Lang, "Algebra" , Addison-Wesley (1974) {{MR|0783636}} {{ZBL|0712.00001}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> E. Artin, "Geometric algebra" , Interscience (1957) {{MR|1529733}} {{MR|0082463}} {{ZBL|0077.02101}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> J.A. Dieudonné, "La géométrie des groups classiques" , Springer (1955) {{MR|}} {{ZBL|0221.20056}} </TD></TR></table> |
| Line 54: | Line 54: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> J. Milnor, D. Husemoller, "Symmetric bilinear forms" , Springer (1973) pp. 16 {{MR|0506372}} {{ZBL|0292.10016}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> T.Y. Lam, "The algebraic theory of quadratic forms" , Benjamin (1973) {{MR|0396410}} {{ZBL|0259.10019}} </TD></TR></table> |
Revision as of 17:35, 31 March 2012
of a vector space
A decomposition of the space into a direct sum of three subspaces having certain properties. More exactly, let  be a vector space over a field
be a vector space over a field  with characteristic different from 2, provided with a metric structure by means of a symmetric or skew-symmetric bilinear form
with characteristic different from 2, provided with a metric structure by means of a symmetric or skew-symmetric bilinear form  . The direct decomposition
. The direct decomposition
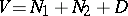 |
is said to be a Witt decomposition of  if
if  and
and  are totally isotropic, while
are totally isotropic, while  is anisotropic and is orthogonal to
is anisotropic and is orthogonal to 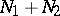 with respect to
with respect to 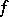 . The Witt decomposition plays an important role in the study of the structure of the form
. The Witt decomposition plays an important role in the study of the structure of the form 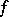 and in problems of classification of bilinear forms.
and in problems of classification of bilinear forms.
Let 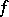 be a non-degenerate bilinear form and let
be a non-degenerate bilinear form and let 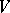 be finite-dimensional. Then any maximal totally isotropic subspace in
be finite-dimensional. Then any maximal totally isotropic subspace in 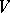 may be included in a Witt decomposition of
may be included in a Witt decomposition of 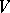 as
as 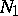 or
or  . For any Witt decomposition
. For any Witt decomposition  , and for any basis
, and for any basis 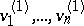 in
in 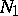 , there exists a basis
, there exists a basis 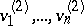 in
in 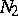 such that
such that  (
( are the Kronecker symbols). For any two Witt decompositions
are the Kronecker symbols). For any two Witt decompositions
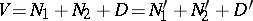 |
the condition 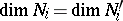 ,
, 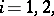 is necessary and sufficient for the existence of a metric automorphism
is necessary and sufficient for the existence of a metric automorphism 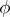 of
of 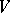 such that
such that
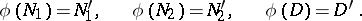 |
A non-degenerate symmetric or skew-symmetric bilinear form 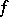 on
on 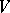 is said to be neutral if
is said to be neutral if 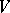 is finite-dimensional and has a Witt decomposition with
is finite-dimensional and has a Witt decomposition with  . In this case the symmetric form is said to be a hyperbolic form, while
. In this case the symmetric form is said to be a hyperbolic form, while  is said to be a hyperbolic space. An orthogonal direct sum of neutral forms is neutral. The matrix of a neutral form (in the basis
is said to be a hyperbolic space. An orthogonal direct sum of neutral forms is neutral. The matrix of a neutral form (in the basis 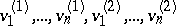 of the space
of the space 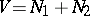 described above) looks like
described above) looks like
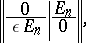 |
where 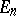 is the identity matrix of order
is the identity matrix of order  , while
, while 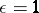 for a symmetric form and
for a symmetric form and 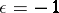 for a skew-symmetric form. Two neutral forms are isometric if and only if they have the same rank. The class of neutral symmetric bilinear forms is the zero (i.e. the neutral element for addition) in the Witt ring of the field
for a skew-symmetric form. Two neutral forms are isometric if and only if they have the same rank. The class of neutral symmetric bilinear forms is the zero (i.e. the neutral element for addition) in the Witt ring of the field 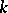 . Neutral forms and only such forms have Witt index
. Neutral forms and only such forms have Witt index 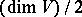 . A skew-symmetric form on a finite-dimensional space is neutral.
. A skew-symmetric form on a finite-dimensional space is neutral.
If 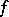 is a non-degenerate symmetric bilinear form on a finite-dimensional space
is a non-degenerate symmetric bilinear form on a finite-dimensional space 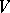 and
and 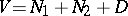 is a Witt decomposition in which
is a Witt decomposition in which 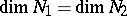 is equal to the Witt index of
is equal to the Witt index of 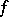 , the restriction of
, the restriction of 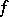 to
to  is a definite, or anisotropic, bilinear form, i.e. is such that
is a definite, or anisotropic, bilinear form, i.e. is such that  for all non-zero
for all non-zero  . This form is independent (apart from an isometry) of the choice of the Witt decomposition of
. This form is independent (apart from an isometry) of the choice of the Witt decomposition of 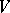 . In the set of definite bilinear forms it is possible to introduce an addition, converting it into an Abelian group — the Witt group of
. In the set of definite bilinear forms it is possible to introduce an addition, converting it into an Abelian group — the Witt group of 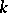 (cf. Witt ring).
(cf. Witt ring).
Let 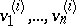 be bases in
be bases in 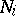 ,
, 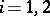 , such that
, such that 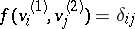 ; the union of these bases with an arbitrary basis in
; the union of these bases with an arbitrary basis in 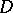 yields a basis in
yields a basis in  in which the matrix of
in which the matrix of 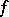 looks like
looks like
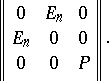 |
For symmetric bilinear forms there exists an orthogonal basis in 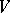 , i.e. a basis in which the matrix of the form is diagonal. If the field
, i.e. a basis in which the matrix of the form is diagonal. If the field 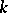 is algebraically closed, there even exists an orthonormal basis (a basis in which the matrix of the form is the identity), and for this reason two non-degenerate symmetric bilinear forms of finite rank over
is algebraically closed, there even exists an orthonormal basis (a basis in which the matrix of the form is the identity), and for this reason two non-degenerate symmetric bilinear forms of finite rank over 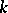 are isometric if and only if they have the same rank. In the general case the classification of such forms substantially depends on the arithmetical properties of the field
are isometric if and only if they have the same rank. In the general case the classification of such forms substantially depends on the arithmetical properties of the field  .
.
The study and classification of degenerate symmetric and skew-symmetric forms can be reduced to the study of non-degenerate forms (the restriction of the form to a subspace which is complementary to the kernel of the form).
All what has been said above permits a generalization to the case of  -Hermitian forms over a skew-field with property
-Hermitian forms over a skew-field with property  (cf. Witt theorem), and also to the case of symmetric bilinear forms associated with quadratic forms, without restrictions on the characteristic of the field.
(cf. Witt theorem), and also to the case of symmetric bilinear forms associated with quadratic forms, without restrictions on the characteristic of the field.
References
| [1] | N. Bourbaki, "Algebra" , Elements of mathematics , 1 , Addison-Wesley (1974) pp. Chapts. 1–2 (Translated from French) MR0354207 Zbl 0281.00006 |
| [2] | S. Lang, "Algebra" , Addison-Wesley (1974) MR0783636 Zbl 0712.00001 |
| [3] | E. Artin, "Geometric algebra" , Interscience (1957) MR1529733 MR0082463 Zbl 0077.02101 |
| [4] | J.A. Dieudonné, "La géométrie des groups classiques" , Springer (1955) Zbl 0221.20056 |
Comments
A vector space with a neutral non-degenerate bilinear form on it is called split or metabolic.
A different form of the Witt decomposition theorem gives a decomposition of a quadratic space 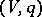 (i.e. a vector space
(i.e. a vector space  with a quadratic form
with a quadratic form  on it) into an orthogonal sum
on it) into an orthogonal sum
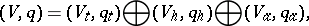 | (*) |
with 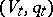 totally isotropic,
totally isotropic, 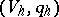 hyperbolic and
hyperbolic and  anisotropic. Moreover, the isometry classes of
anisotropic. Moreover, the isometry classes of 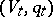 ,
,  and
and 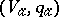 are uniquely determined by that of
are uniquely determined by that of 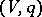 .
.
In this decomposition, 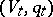 is the radical of
is the radical of  ,
, 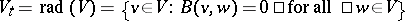 , where
, where 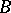 is the symmetric bilinear form on
is the symmetric bilinear form on 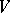 associated to
associated to 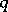 :
:
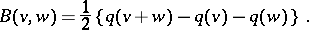 |
The uniqueness of the factors in the Witt decomposition (*) follows from the Witt cancellation theorem, which says that if  is isometric to
is isometric to 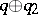 , then
, then  and
and 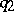 are isometric.
are isometric.
References
| [a1] | J. Milnor, D. Husemoller, "Symmetric bilinear forms" , Springer (1973) pp. 16 MR0506372 Zbl 0292.10016 |
| [a2] | T.Y. Lam, "The algebraic theory of quadratic forms" , Benjamin (1973) MR0396410 Zbl 0259.10019 |
Witt decomposition. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Witt_decomposition&oldid=17145