Hermite problem

The problem about the homogeneous arithmetical minima of positive -ary quadratic forms with real coefficients. It is equivalent to the problem of the densest lattice packing of -dimensional balls of equal radius (see Geometry of numbers).

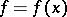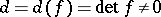Let , , be a positive quadratic form over of determinant ; and let

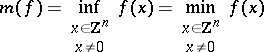be its homogeneous arithmetical minimum. The quantity

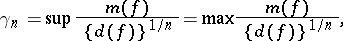where the supermum or maximum is over all positive quadratic forms 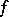, is called the Hermite constant; 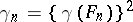, where 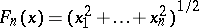is the radial function corresponding to a ball.

Originally, one understood by the Hermite problem the task of finding or estimating 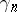(from above and below). The exact values of 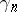are known only for (see [1]). For estimates of 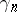, see [2] or [1].

Subsequently, the term Hermite problem was used for the search for local maxima (boundary or extremal) of 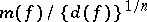in the space of coefficients and their corresponding forms 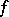. Algorithms are known for finding all classes of boundary forms. In particular, the Voronoi algorithm for perfect forms (see [1], [3], [4]).

The problem was posed by Ch. Hermite in 1850.

References

[1]	P.M. Gruber, C.G. Lekkerkerker, "Geometry of numbers" , North-Holland (1987) (Updated reprint) MR0893813 Zbl 0611.10017
[2]	C.A. Rogers, "Packing and covering" , Cambridge Univ. Press (1964) MR0172183 Zbl 0176.51401
[3]	B.N. Delone, "The Peterburg school of number theory" , Moscow-Leningrad (1947) (In Russian)
[4]	E.P. Baranovskii, "Packings, coverings, partitionings and certain other distributions in spaces of constant curvature" Progress in Math. , 9 (1971) pp. 209–253 Itogi Nauk. Mat. Algebra Topol. Geom. 1967 (1969) pp. 189–225