Difference between revisions of "Specialization of a point"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 6: | Line 6: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> Yu.I. Manin, "Lectures on algebraic geometry" , '''1''' , Moscow (1970) (In Russian) {{MR|0284434}} {{ZBL|0204.21302}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> A. Grothendieck, J. Dieudonné, "Eléments de géometrie algébrique" , '''I. Le langage des schémes''' , Springer (1971) {{MR|0217085}} {ZBL|0203.23301}} </TD></TR></table> |
| Line 14: | Line 14: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> R. Hartshorne, "Algebraic geometry" , Springer (1977) pp. Sect. IV.2 {{MR|0463157}} {{ZBL|0367.14001}} </TD></TR></table> |
Revision as of 21:56, 30 March 2012
 of a topological space
of a topological space 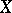
A point 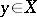 for which the inclusion
for which the inclusion 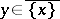 holds (this is equivalent to the inclusion
holds (this is equivalent to the inclusion 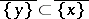 ). A point
). A point  is called generic if any point of
is called generic if any point of 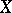 is a specialization of it, that is, if
is a specialization of it, that is, if 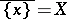 . The other extreme case is that of a closed point: A point which has a unique specialization, namely the point itself.
. The other extreme case is that of a closed point: A point which has a unique specialization, namely the point itself.
For the affine scheme 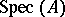 of a ring
of a ring 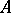 , a point
, a point 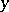 is a specialization of a point
is a specialization of a point  if for the corresponding prime ideals of
if for the corresponding prime ideals of 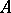 the inclusion
the inclusion 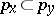 holds. When
holds. When 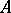 is a ring without zero divisors, the point
is a ring without zero divisors, the point 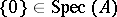 is the generic one. The relation of specialization distributes into levels: the highest are the closed points, on the next level are the points whose specializations are closed, and on the
is the generic one. The relation of specialization distributes into levels: the highest are the closed points, on the next level are the points whose specializations are closed, and on the 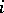 -th level are the points whose specializations belong to the levels with labels
-th level are the points whose specializations belong to the levels with labels 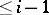 . For example, for
. For example, for 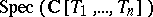 there are
there are 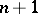 levels: closed points, generic points of curves, generic points of surfaces
levels: closed points, generic points of curves, generic points of surfaces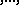 the generic point of the
the generic point of the  -dimensional affine space.
-dimensional affine space.
References
| [1] | Yu.I. Manin, "Lectures on algebraic geometry" , 1 , Moscow (1970) (In Russian) MR0284434 Zbl 0204.21302 |
| [2] | A. Grothendieck, J. Dieudonné, "Eléments de géometrie algébrique" , I. Le langage des schémes , Springer (1971) MR0217085 {ZBL|0203.23301}} |
Comments
Of course, 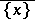 denotes the closure of the set
denotes the closure of the set 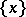 . The closure of a point is an irreducible subset of
. The closure of a point is an irreducible subset of 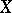 , and conversely, every irreducible subset of
, and conversely, every irreducible subset of 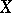 has a generic point.
has a generic point.
References
| [a1] | R. Hartshorne, "Algebraic geometry" , Springer (1977) pp. Sect. IV.2 MR0463157 Zbl 0367.14001 |
Specialization of a point. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Specialization_of_a_point&oldid=15043