Difference between revisions of "Quasi-affine scheme"
From Encyclopedia of Mathematics
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 7: | Line 7: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> A. Grothendieck, "Étude globale élémentaire de quelques classes de morphismes" ''Publ. Math. IHES'' , '''8''' (1961) pp. Sect. 5.1 {{MR|0217084}} {{MR|0163909}} {{ZBL|0118.36206}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> R. Hartshorne, "Algebraic geometry" , Springer (1977) pp. 3, 21 {{MR|0463157}} {{ZBL|0367.14001}} </TD></TR></table> |
Revision as of 21:55, 30 March 2012
A scheme isomorphic to an open compact subscheme of an affine scheme. A compact scheme 
is quasi-affine if and only if one of the following equivalent conditions holds: 1) the canonical morphism 
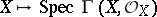is an open imbedding; and 2) any quasi-coherent sheaf of 
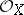-modules is generated by global sections. A morphism of schemes 
is called quasi-affine if for any open affine subscheme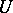 
in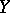 
the inverse image 
is a quasi-affine scheme.
Comments
A quasi-affine variety is an open subvariety of an affine algebraic variety. (As an open subspace of a Noetherian space it is automatically compact.) An example of a quasi-affine variety that is not affine is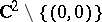 
.
References
| [a1] | A. Grothendieck, "Étude globale élémentaire de quelques classes de morphismes" Publ. Math. IHES , 8 (1961) pp. Sect. 5.1 MR0217084 MR0163909 Zbl 0118.36206 |
| [a2] | R. Hartshorne, "Algebraic geometry" , Springer (1977) pp. 3, 21 MR0463157 Zbl 0367.14001 |
How to Cite This Entry:
Quasi-affine scheme. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Quasi-affine_scheme&oldid=17637
Quasi-affine scheme. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Quasi-affine_scheme&oldid=17637
This article was adapted from an original article by V.I. Danilov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article