Difference between revisions of "Generic set"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 4: | Line 4: | ||
====Comments==== | ====Comments==== | ||
| − | The phrase | + | The phrase "generic set" as defined above is used mostly in differential topology and the theory of dynamical systems, where a property is said to hold generically if it holds for, say, a generic set of parameters. |
| − | It is more common to call (a set containing) an intersection of countably many dense open sets residual or comeager, for its complement is meager: a union of countably many nowhere-dense sets (cf. [[Nowhere-dense set|Nowhere-dense set]]). Meager sets are considered topologically negligible, so that the Russian phrase | + | It is more common to call (a set containing) an intersection of countably many dense open sets residual or comeager, for its complement is meager: a union of countably many nowhere-dense sets (cf. [[Nowhere-dense set|Nowhere-dense set]]). Meager sets are considered topologically negligible, so that the Russian phrase "massive set" aptly describes this kind of set. The Baire category theorem (cf. [[Baire theorem|Baire theorem]]) says that in completely-metrizable spaces residual sets are dense; this is also true for locally compact spaces. |
| − | In [[Mathematical logic|mathematical logic]] and [[Set theory|set theory]] the term | + | In [[Mathematical logic|mathematical logic]] and [[Set theory|set theory]] the term "generic set" is also used. It refers to a "general" set of conditions which is consistent and is also such that every sentence from a specified set of sentences is decided. |
The probably best-known example is found in forcing in set theory (cf. [[Forcing method|Forcing method]]). Here the full set of conditions is a [[Partially ordered set|partially ordered set]] and a generic set is then a [[Filter|filter]] which intersects all sets from a certain collection of dense sets. Another example occurs in model-theoretic forcing, where conditions are finite consistent sets of atomic sentences or negations of such. | The probably best-known example is found in forcing in set theory (cf. [[Forcing method|Forcing method]]). Here the full set of conditions is a [[Partially ordered set|partially ordered set]] and a generic set is then a [[Filter|filter]] which intersects all sets from a certain collection of dense sets. Another example occurs in model-theoretic forcing, where conditions are finite consistent sets of atomic sentences or negations of such. | ||
| Line 14: | Line 14: | ||
In many instances the set of sentences to be decided is countable and the collection of maximally-consistent sets of conditions is a compact topological space. One can then invoke the Baire category theorem to conclude that the collection of generic sets is actually a dense generic set in the sense of the main article above. | In many instances the set of sentences to be decided is countable and the collection of maximally-consistent sets of conditions is a compact topological space. One can then invoke the Baire category theorem to conclude that the collection of generic sets is actually a dense generic set in the sense of the main article above. | ||
| − | In algebraic (and analytic) geometry, when dealing with a [[Scheme|scheme]] or pre-scheme with the [[Zariski topology|Zariski topology]] a generic set usually means | + | In algebraic (and analytic) geometry, when dealing with a [[Scheme|scheme]] or pre-scheme with the [[Zariski topology|Zariski topology]] a generic set usually means "containing a dense open set" or, what is often the same, the complement of a set of lower dimension. Thus, if one is dealing with a family of objects parametrized locally by a complex manifold or an analytic or algebraic variety, then the statement that a member of this family has a certain property generically or that a generic member of the family has the property means that the set of members of the family not having the property is contained in a subvariety of strictly lower dimension. For instance, the generic smoothness result says that if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043960/g0439606.png" /> is a morphism of varieties over an algebraically closed field of characteristic zero and if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043960/g0439607.png" /> is non-singular, then there is a non-empty open subset <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043960/g0439608.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043960/g0439609.png" /> is smooth. |
Cf. also [[Generic point|Generic point]]. | Cf. also [[Generic point|Generic point]]. | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> K. Kunen, "Set theory" , North-Holland (1980) {{MR|1567279}} {{MR|0597342}} {{ZBL|0443.03021}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> J. Barwise (ed.) , ''Handbook of mathematical logic'' , North-Holland (1977) ((especially the article of D.A. Martin on Descriptive set theory)) {{MR|0457132}} {{ZBL|0623.03003}} {{ZBL|0623.03002}} {{ZBL|0528.03001}} {{ZBL|0443.03001}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> Ph.A. Griffiths, "Principles of algebraic geometry" , Wiley (Interscience) (1978) pp. 20 ff {{MR|0507725}} {{ZBL|0408.14001}} </TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> R. Hartshorne, "Algebraic geometry" , Springer (1977) pp. 272 {{MR|0463157}} {{ZBL|0367.14001}} </TD></TR></table> |
Revision as of 21:52, 30 March 2012
A set 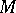 in a topological space
in a topological space  that is the intersection of a countable number of open dense subsets in
that is the intersection of a countable number of open dense subsets in 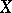 . If each generic set is dense in
. If each generic set is dense in  , then
, then 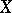 is called a Baire space.
is called a Baire space.
Comments
The phrase "generic set" as defined above is used mostly in differential topology and the theory of dynamical systems, where a property is said to hold generically if it holds for, say, a generic set of parameters.
It is more common to call (a set containing) an intersection of countably many dense open sets residual or comeager, for its complement is meager: a union of countably many nowhere-dense sets (cf. Nowhere-dense set). Meager sets are considered topologically negligible, so that the Russian phrase "massive set" aptly describes this kind of set. The Baire category theorem (cf. Baire theorem) says that in completely-metrizable spaces residual sets are dense; this is also true for locally compact spaces.
In mathematical logic and set theory the term "generic set" is also used. It refers to a "general" set of conditions which is consistent and is also such that every sentence from a specified set of sentences is decided.
The probably best-known example is found in forcing in set theory (cf. Forcing method). Here the full set of conditions is a partially ordered set and a generic set is then a filter which intersects all sets from a certain collection of dense sets. Another example occurs in model-theoretic forcing, where conditions are finite consistent sets of atomic sentences or negations of such.
In many instances the set of sentences to be decided is countable and the collection of maximally-consistent sets of conditions is a compact topological space. One can then invoke the Baire category theorem to conclude that the collection of generic sets is actually a dense generic set in the sense of the main article above.
In algebraic (and analytic) geometry, when dealing with a scheme or pre-scheme with the Zariski topology a generic set usually means "containing a dense open set" or, what is often the same, the complement of a set of lower dimension. Thus, if one is dealing with a family of objects parametrized locally by a complex manifold or an analytic or algebraic variety, then the statement that a member of this family has a certain property generically or that a generic member of the family has the property means that the set of members of the family not having the property is contained in a subvariety of strictly lower dimension. For instance, the generic smoothness result says that if  is a morphism of varieties over an algebraically closed field of characteristic zero and if
is a morphism of varieties over an algebraically closed field of characteristic zero and if  is non-singular, then there is a non-empty open subset
is non-singular, then there is a non-empty open subset 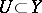 such that
such that 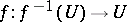 is smooth.
is smooth.
Cf. also Generic point.
References
| [a1] | K. Kunen, "Set theory" , North-Holland (1980) MR1567279 MR0597342 Zbl 0443.03021 |
| [a2] | J. Barwise (ed.) , Handbook of mathematical logic , North-Holland (1977) ((especially the article of D.A. Martin on Descriptive set theory)) MR0457132 Zbl 0623.03003 Zbl 0623.03002 Zbl 0528.03001 Zbl 0443.03001 |
| [a3] | Ph.A. Griffiths, "Principles of algebraic geometry" , Wiley (Interscience) (1978) pp. 20 ff MR0507725 Zbl 0408.14001 |
| [a4] | R. Hartshorne, "Algebraic geometry" , Springer (1977) pp. 272 MR0463157 Zbl 0367.14001 |
Generic set. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Generic_set&oldid=12467