Difference between revisions of "Cusp"
From Encyclopedia of Mathematics
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 7: | Line 7: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> W. Fulton, "Algebraic curves. An introduction to algebraic geometry" , Benjamin (1969) pp. 66 {{MR|0313252}} {{ZBL|0681.14011}} </TD></TR></table> |
Revision as of 21:51, 30 March 2012
ordinary cusp
A singular point of specific type of an algebraic curve. Namely, a singular point  of an algebraic curve
of an algebraic curve 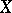 over an algebraically closed field
over an algebraically closed field 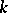 is called a cusp if the completion of its local ring
is called a cusp if the completion of its local ring 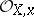 is isomorphic to the completion of the local ring of the plane algebraic curve
is isomorphic to the completion of the local ring of the plane algebraic curve 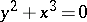 at the origin.
at the origin.
Comments
A cusp can also be defined via the so-called intersection number of two plane curves at a point, cf. [a1], pp. 74-82. A generalization of a cusp is a hypercusp, cf. [a1], p. 82.
References
| [a1] | W. Fulton, "Algebraic curves. An introduction to algebraic geometry" , Benjamin (1969) pp. 66 MR0313252 Zbl 0681.14011 |
How to Cite This Entry:
Cusp. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cusp&oldid=18769
Cusp. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cusp&oldid=18769