Difference between revisions of "Closed subscheme"
From Encyclopedia of Mathematics
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 7: | Line 7: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> R. Hartshorne, "Algebraic geometry" , Springer (1977) {{MR|0463157}} {{ZBL|0367.14001}} </TD></TR></table> |
Revision as of 21:50, 30 March 2012
A subscheme of a scheme 
defined by a quasi-coherent sheaf of ideals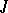 
of the structure sheaf 
as follows: The topological space of the subscheme,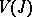 
, is the support of the quotient sheaf 
, and the structure sheaf is the restriction of 
to its support. A morphism of schemes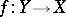 
is called a closed imbedding if 
is an isomorphism of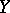 
onto some closed subscheme in 
; a closed imbedding is a monomorphism in the category of schemes. For any closed subset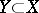 
there exists a minimal closed subscheme in 
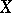with space 
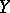, known as the reduced closed subscheme with space 
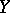. If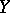 
is a subscheme of 
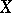, then the smallest closed subscheme 
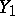of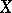 
containing 
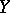is known as the (schematic) closure of the subscheme 
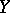in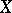 
.
Comments
References
| [a1] | R. Hartshorne, "Algebraic geometry" , Springer (1977) MR0463157 Zbl 0367.14001 |
How to Cite This Entry:
Closed subscheme. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Closed_subscheme&oldid=17023
Closed subscheme. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Closed_subscheme&oldid=17023
This article was adapted from an original article by V.I. Danilov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article