Difference between revisions of "Poincaré problem"
From Encyclopedia of Mathematics
Ulf Rehmann (talk | contribs) m (moved Poincaré problem to Poincare problem: ascii title) |
Ulf Rehmann (talk | contribs) m (moved Poincare problem to Poincaré problem over redirect: accented title) |
(No difference)
| |
Revision as of 07:55, 26 March 2012
To find a harmonic function in a bounded simply-connected domain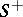 
which, on the boundary 
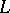of the domain, satisfies the condition
 |
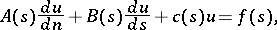where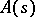 
, 
, 
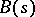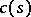, and 
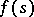are real-valued functions given on 
, 
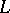is the arc parameter and 
is the normal to 
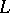. H. Poincaré (1910) arrived at this problem while working on the mathematical theory of fluid flow and gave an (incomplete) solution to the problem in case 
, 
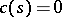and the contour 
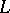and the functions 
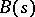and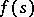 
are analytic.
See also Boundary value problems of analytic function theory.
How to Cite This Entry:
Poincaré problem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Poincar%C3%A9_problem&oldid=22937
Poincaré problem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Poincar%C3%A9_problem&oldid=22937
This article was adapted from an original article by A.B. Ivanov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article