Difference between revisions of "Fréchet surface"
Ulf Rehmann (talk | contribs) m (moved Fréchet surface to Frechet surface: ascii title) |
Ulf Rehmann (talk | contribs) m (moved Frechet surface to Fréchet surface over redirect: accented title) |
(No difference)
| |
Revision as of 07:54, 26 March 2012
A generalization of the concept of a surface in a Euclidean space to the case of an arbitrary metric space 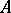 . Let
. Let 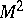 be a compact two-dimensional manifold (either closed or with a boundary). The points of
be a compact two-dimensional manifold (either closed or with a boundary). The points of 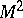 play the role of parameter. Continuous mappings
play the role of parameter. Continuous mappings 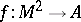 are called parametrized surfaces. Two parametrized surfaces are regarded as equivalent if
are called parametrized surfaces. Two parametrized surfaces are regarded as equivalent if
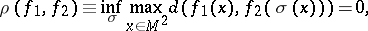 |
where 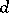 is the distance in
is the distance in 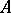 and the
and the 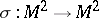 are all possible homeomorphisms of
are all possible homeomorphisms of 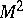 onto itself. A class of equivalent parametrized surfaces is called a Fréchet surface (see [1]), and each of the parametrized surfaces in this class is called a parametrization of the Fréchet surface. Many properties of parametrized surfaces are properties of the Fréchet surface, and not of its concrete parametrization. For two Fréchet surfaces, the value of
onto itself. A class of equivalent parametrized surfaces is called a Fréchet surface (see [1]), and each of the parametrized surfaces in this class is called a parametrization of the Fréchet surface. Many properties of parametrized surfaces are properties of the Fréchet surface, and not of its concrete parametrization. For two Fréchet surfaces, the value of 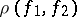 is independent of the choice of the parametrizations
is independent of the choice of the parametrizations 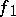 and
and 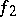 ; it is called the Fréchet distance between the Fréchet surfaces. If one changes the domain
; it is called the Fréchet distance between the Fréchet surfaces. If one changes the domain 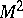 of the parameter in the definition of a Fréchet surface to a circle or a closed interval, one obtains the definition of a Fréchet curve (see [2]).
of the parameter in the definition of a Fréchet surface to a circle or a closed interval, one obtains the definition of a Fréchet curve (see [2]).
References
| [1] | M. Fréchet, Ann. Soc. Polon. Math. , 3 (1924) pp. 4–19 |
| [2] | M. Fréchet, "Sur quelques points du calcul fonctionnel" Rend. Circolo Mat. Palermo , 74 (1906) pp. 1–74 |
Fréchet surface. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fr%C3%A9chet_surface&oldid=22461