Difference between revisions of "Calderón-Toeplitz operator"
Ulf Rehmann (talk | contribs) m (moved Calderón–Toeplitz operator to Calderon-Toeplitz operator: ascii title) |
Ulf Rehmann (talk | contribs) m (moved Calderon-Toeplitz operator to Calderón-Toeplitz operator: accented title) |
(No difference)
| |
Revision as of 07:54, 26 March 2012
An integral operator depending on two function parameters, 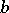 and
and 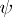 , and defined by the formula
, and defined by the formula
 |
where 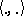 is the inner product in
is the inner product in 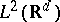 (the space of square-integrable functions),
(the space of square-integrable functions), 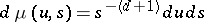 , and
, and 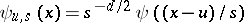 .
.
For  and
and 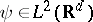 satisfying the admissibility condition (i.e., for almost-every
satisfying the admissibility condition (i.e., for almost-every 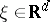 one has
one has 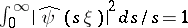 ,
,  being the Fourier transform of
being the Fourier transform of 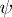 ), the operator
), the operator  becomes the identity. The formula
becomes the identity. The formula 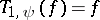 is known as the Calderón reproducing formula.
is known as the Calderón reproducing formula.
The name "Calderón–Toeplitz operator" comes from the fact that 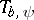 (for admissible
(for admissible 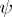 ) is unitarily equivalent to the Toeplitz-type operator
) is unitarily equivalent to the Toeplitz-type operator
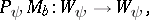 |
where 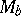 denotes the operator of multiplication by
denotes the operator of multiplication by 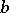 and
and 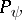 is the orthogonal projection from
is the orthogonal projection from 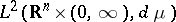 onto its closed subspace
onto its closed subspace 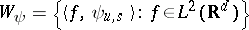 , called the space of Calderón transforms.
, called the space of Calderón transforms.
Calderón–Toeplitz operators were introduced by R. Rochberg in [a4] as a wavelet counterpart of Toeplitz operators defined on Hilbert spaces of holomorphic functions. They are the model operators that fit nicely in the context of wavelet decomposition of function spaces and almost diagonalization of operators (cf. also Wavelet analysis). They also are an effective time-frequency localization tool [a1].
Properties of the mapping 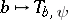 for fixed, sufficiently smooth,
for fixed, sufficiently smooth, 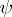 are:
are:
1) (correspondence principle, [a5]). Suppose that 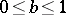 . Then
. Then 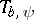 is bounded, self-adjoint and
is bounded, self-adjoint and 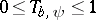 . Let
. Let 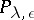 be the spectral projection associated with the interval
be the spectral projection associated with the interval  . For any
. For any 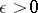 there is an
there is an 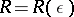 so that if
so that if 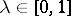 and
and 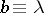 on
on 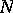 disjoint hyperbolic balls of radius
disjoint hyperbolic balls of radius 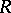 , then the dimension of the range of
, then the dimension of the range of 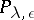 is at least
is at least 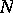 .
.
2) ([a2]). Let 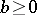 and
and 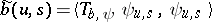 .
.
i) (boundedness). The operator 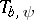 is bounded if and only if
is bounded if and only if 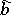 is bounded.
is bounded.
ii) (compactness). The operator 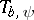 is compact if and only if
is compact if and only if 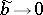 at infinity.
at infinity.
iii) (Schatten ideal behaviour). If 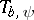 is compact, then for
is compact, then for 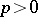 ,
,
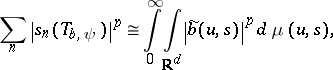 |
where
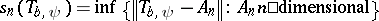 |
and the symbol 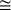 means that the quotient is bounded above and below with constants independent of
means that the quotient is bounded above and below with constants independent of 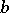 .
.
The eigenvalues of  can be estimated as follows ([a6], [a3]).
can be estimated as follows ([a6], [a3]).
Suppose that 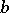 ,
, 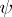 have compact support,
have compact support, 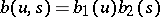 being smooth with
being smooth with 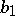 ,
, 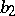 both non-negative, and suppose that the support of the kernel of
both non-negative, and suppose that the support of the kernel of  is contained in a cube of side length one. Let
is contained in a cube of side length one. Let  be the non-increasing rearrangement (with respect to
be the non-increasing rearrangement (with respect to 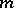 ) of the sequence
) of the sequence
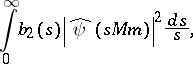 |
where 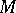 is a natural number,
is a natural number, 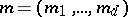 , and
, and  are integers. There are positive constants
are integers. There are positive constants  ,
, 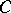 and a natural number
and a natural number 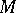 such that
such that
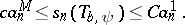 |
In particular, for 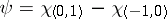 the eigenvalues satisfy two-sided estimates:
the eigenvalues satisfy two-sided estimates: 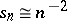 .
.
References
| [a1] | I. Daubechies, "Ten lectures on wavelets" , CBMS-NSF Regional Conf. Ser. , 6 , SIAM (1992) |
| [a2] | K. Nowak, "On Calderón–Toeplitz operators" Monatsh. Math. , 116 (1993) pp. 49–72 |
| [a3] | K. Nowak, "Some eigenvalue estimates for wavelet related Toeplitz operators" Colloq. Math. , LXV (1993) pp. 149–156 |
| [a4] | R. Rochberg, "Toeplitz and Hankel operators, wavelets, NWO sequences and almost diagonalization of operators" W.B. Arveson (ed.) R.G. Douglas (ed.) , Proc. Symp. Pure Math. , 51 , Amer. Math. Soc. (1990) pp. 425–444 |
| [a5] | R. Rochberg, "A correspondence principle for Toeplitz and Calderón–Toeplitz operators" M. Cwikel (ed.) etAAsal. (ed.) , Israel Math. Conf. Proc. , 5 (1992) pp. 229–243 |
| [a6] | R. Rochberg, "Eigenvalue estimates for Calderón–Toeplitz operators" K. Jarosz (ed.) , Lecture Notes in Pure and Appl. Math. , 136 , M. Dekker (1992) pp. 345–357 |
Calderón-Toeplitz operator. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Calder%C3%B3n-Toeplitz_operator&oldid=22227