Difference between revisions of "Neyman-Pearson lemma"
From Encyclopedia of Mathematics
(Importing text file) |
Ulf Rehmann (talk | contribs) m (moved Neyman–Pearson lemma to Neyman-Pearson lemma: ascii title) |
(No difference)
| |
Revision as of 18:53, 24 March 2012
A lemma asserting that in the problem of statistically testing a simple hypothesis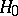 
against a simple alternative 
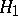the likelihood-ratio test is a most-powerful test among all statistical tests having one and the same given significance level. It was proved by J. Neyman and E.S. Pearson [1]. It is often called the fundamental lemma of mathematical statistics. See also Statistical hypotheses, verification of.
References
| [1] | J. Neyman, E.S. Pearson, "On the problem of the most efficient tests of statistical hypotheses" Philos. Trans. Roy. Soc. London Ser. A. , 231 (1933) pp. 289–337 |
| [2] | E.L. Lehmann, "Statistical hypotheses testing" , Wiley (1978) |
How to Cite This Entry:
Neyman-Pearson lemma. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Neyman-Pearson_lemma&oldid=16551
Neyman-Pearson lemma. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Neyman-Pearson_lemma&oldid=16551
This article was adapted from an original article by M.S. Nikulin (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article