Difference between revisions of "Mehler-Fock transform"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (moved Mehler–Fock transform to Mehler-Fock transform: ascii title) |
Revision as of 18:53, 24 March 2012
Mehler–Fok transform
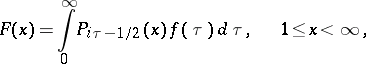 | (1) |
where 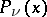 is the Legendre function of the first kind (cf. Legendre functions). If
is the Legendre function of the first kind (cf. Legendre functions). If 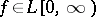 , the function
, the function 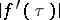 is locally integrable on
is locally integrable on 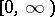 and
and 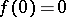 , then the following inversion formula is valid:
, then the following inversion formula is valid:
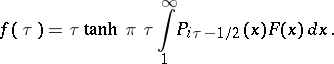 | (2) |
The Parseval identity. Consider the Mehler–Fock transform and its inverse defined by the equalities
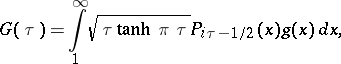 |
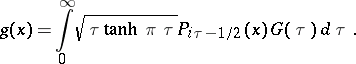 |
If 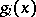 ,
, 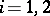 , are arbitrary real-valued functions satisfying the conditions
, are arbitrary real-valued functions satisfying the conditions
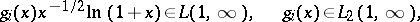 |
then
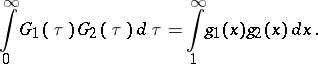 |
The generalized Mehler–Fock transform and the corresponding inversion formula are:
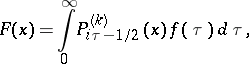 | (3) |
and
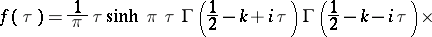 | (4) |
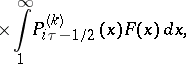 |
where 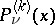 are the associated Legendre functions of the first kind. For
are the associated Legendre functions of the first kind. For 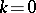 formulas (3) and (4) reduce to (1) and (2); for
formulas (3) and (4) reduce to (1) and (2); for 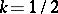 ,
, 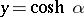 , formulas (3) and (4) lead to the Fourier cosine transform, and for
, formulas (3) and (4) lead to the Fourier cosine transform, and for 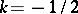 ,
, 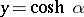 to the Fourier sine transform. The transforms (1) and (2) were introduced by F.G. Mehler [1]. The basic theorems were proved by V.A. Fock [V.A. Fok].
to the Fourier sine transform. The transforms (1) and (2) were introduced by F.G. Mehler [1]. The basic theorems were proved by V.A. Fock [V.A. Fok].
References
| [1] | F.G. Mehler, "Ueber eine mit den Kugel- und Cylinderfunctionen verwandte Function und ihre Anwendung in der Theorie der Electricitätsvertheilung" Math. Ann. , 18 (1881) pp. 161–194 |
| [2] | V.A. Fok, "On the representation of an arbitrary function by an integral involving Legendre functions with complex index" Dokl. Akad. Nauk SSSR , 39 (1943) pp. 253–256 (In Russian) |
| [3] | V.A. Ditkin, A.P. Prudnikov, "Operational calculus" Progress in Math. , 1 (1968) pp. 1–75 Itogi Nauk. Mat. Anal. 1966 (1967) pp. 7–82 |
Comments
References
| [a1] | I.N. Sneddon, "The use of integral transforms" , McGraw-Hill (1972) |
Mehler-Fock transform. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Mehler-Fock_transform&oldid=12375