Levi-Mal'tsev decomposition

The presentation of a finite-dimensional Lie algebra 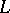over a field of characteristic zero as a direct sum (as vector spaces) of its radical 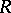(the maximal solvable ideal in 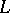) and a semi-simple Lie subalgebra 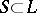. It was obtained by E.E. Levi [1] and A.I. Mal'tsev [2]. The Levi–Mal'tsev theorem states that there always is such a decomposition 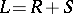; moreover, the subalgebra 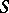is unique up to an automorphism of the form 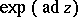, where 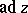is the inner derivation of the Lie algebra 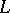determined by an element of the nil radical (the largest nilpotent ideal) o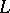f . 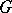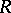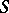If is a connected and simply-connected real Lie group, then there are closed simply-connected analytic subgroups and of 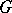, where 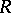is the maximal connected closed solvable normal subgroup of 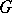, 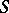is a semi-simple subgroup of 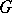, , 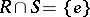such that the mapping 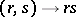, , 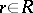, 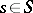is an analytic isomorphism of the manifold 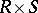onto 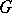; in this case the decomposition 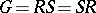is also called a Levi–Mal'tsev decomposition.

References

[1]	E.E. Levi, Atti. Accad. Sci. Torino Cl. Sci. Fis. Mat. Natur. , 40 (1906) pp. 3–17
[2]	A.I. Mal'tsev, "On the representation of an algebra as a direct sum of the radical and a semi-simple subalgebra" Dokl. Akad. Nauk SSSR , 36 : 2 (1942) pp. 42–45 (In Russian)
[3]	N. Jacobson, "Lie algebras" , Interscience (1962) ((also: Dover, reprint, 1979))
[4]	A.A. Kirillov, "Elements of the theory of representations" , Springer (1976) (Translated from Russian)
[5]	M.A. Naimark, "Theory of group representations" , Springer (1982) (Translated from Russian)

Comments

The existence of 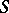, called the Levi factor (if 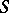is a semi-simple subalgebra, respectively a semi-simple subgroup, also called a Levi subalgebra, respectively Levi subgroup), was established by Levi. The conjugacy of Levi factors was proved by Mal'tsev.

An analogue of the decomposition 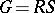holds for an algebraic group 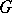. In this case 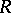is the maximal unipotent normal subgroup and 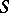is a maximal reductive subgroup (Mostow's theorem).

References

[a1]	N. Bourbaki, "Elements of mathematics. Lie groups and Lie algebras" , Addison-Wesley (1975) (Translated from French)
[a2]	G. Hochschild, "The structure of Lie groups" , Holden-Day (1965)