Ivanov-Petrova metric

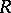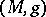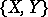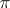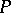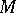Let be the Riemann curvature tensor of a Riemannian manifold . If is an orthonormal basis for an oriented -plane in the tangent space at a point of , let 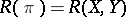be the skew-symmetric curvature operator introduced by R. Ivanova and G. Stanilov [a3]. The Riemannian metric is said to be an Ivanov–Petrova metric if the eigenvalues of 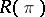depend only on the point 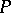but not upon the particular -plane in question.

Example 1.

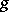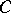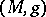If is a metric of constant sectional curvature , then the group of local isometries acts transitively on the Grassmannian of oriented -planes and hence is Ivanov–Petrova. The eigenvalues of 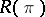are .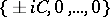

Example 2.

Let 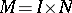be a product manifold, where 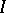is a subinterval of 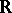and where 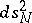is a metric of constant sectional curvature 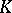on 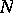. Give 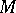the metric

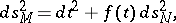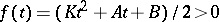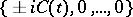where . One can then compute that the eigenvalues of are for 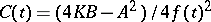. Thus, this metric is Ivanov–Petrova.

In Example 1, the eigenvalues of the skew-symmetric curvature operator are constant; in Example 2, the eigenvalues depend upon the point of the manifold. S. Ivanov and I. Petrova [a2] showed that in dimension 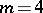, any Riemannian manifold which is Ivanov–Petrova is locally isometric to one of the two metrics exhibited above. This result was later generalized [a4], [a1] to dimensions 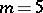, , 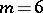and 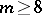; the case 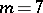is exceptional and is still open (1998). Partial results in the Lorentzian setting have been obtained by T. Zhang [a5].

Let 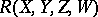be a 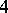-tensor on 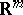which defines a corresponding curvature operator 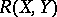. If 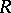satisfies the identities,

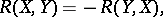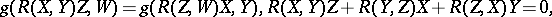then 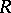is said to be an algebraic curvature tensor. The algebraic curvature tensors which are Ivanov–Petrova have also been classified; they are known to have rank at most in all dimensions except 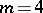and 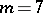, and have the form

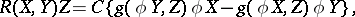where 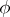is an isometry with 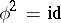. Note that in dimension 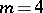, there is an algebraic curvature tensor which is Ivanov–Petrova, has rank 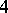and which is constructed using the quaternions; up to scaling and change of basis it is unique and the non-zero entries (up to the usual curvature symmetries) are given by:

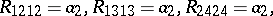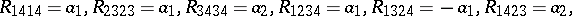where 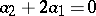. The situation in dimension 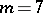is open (1998).

References

[a1]	P. Gilkey, J.V. Leahy, H. Sadofsky, "Riemannian manifolds whose skew-symmetric curvature operator has constant eigenvalues" Indiana J. (to appear)
[a2]	S. Ivanov, I. Petrova, "Riemannian manifold in which the skew-symmetric curvature operator has pointwise constant eigenvalues" Geom. Dedicata , 70 (1998) pp. 269–282
[a3]	R. Ivanova, G. Stanilov, "A skew-symmetric curvature operator in Riemannian geometry" M. Behara (ed.) R. Fritsch (ed.) R. Lintz (ed.) , Symposia Gaussiana, Conf. A (1995) pp. 391–395
[a4]	P. Gilkey, "Riemannian manifolds whose skew-symmetric curvature operator has constant eigenvalues II" , Proc. Diff. Geom. Symp. (Brno, 1998) (to appear)
[a5]	T. Zhang, "Manifolds with indefinite metrics whose skew symmetric curvature operator has constant eigenvalues" PhD Thesis Univ. Oregon (2000)