Difference between revisions of "Gromov-Lawson conjecture"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (moved Gromov–Lawson conjecture to Gromov-Lawson conjecture: ascii title) |
(No difference)
| |
Revision as of 18:52, 24 March 2012
If 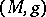 is a metric of positive scalar curvature (cf. also Metric) on a compact spin manifold (cf. also Spinor structure), results of A. Lichnerowicz [a4] show that there are no harmonic spinors; consequently, the
is a metric of positive scalar curvature (cf. also Metric) on a compact spin manifold (cf. also Spinor structure), results of A. Lichnerowicz [a4] show that there are no harmonic spinors; consequently, the 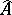 -genus of
-genus of 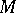 vanishes. M. Gromov and H.B. Lawson [a2], [a3] showed that if a manifold
vanishes. M. Gromov and H.B. Lawson [a2], [a3] showed that if a manifold 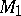 can be obtained from a manifold
can be obtained from a manifold 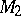 which admits a metric of positive scalar curvature, by surgeries in codimension at least
which admits a metric of positive scalar curvature, by surgeries in codimension at least  , then
, then  admits a metric of positive scalar curvature. They wondered if this might be the only obstruction to the existence of a metric of positive scalar curvature in the spinor context if the dimension
admits a metric of positive scalar curvature. They wondered if this might be the only obstruction to the existence of a metric of positive scalar curvature in the spinor context if the dimension 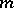 was at least
was at least  . (This restriction is necessary to ensure that certain surgery arguments work.) S. Stolz [a9] showed this was the case in the simply-connected setting: if
. (This restriction is necessary to ensure that certain surgery arguments work.) S. Stolz [a9] showed this was the case in the simply-connected setting: if 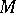 is a simply-connected spin manifold of dimension at least
is a simply-connected spin manifold of dimension at least  (cf. also Simply-connected domain), then
(cf. also Simply-connected domain), then 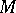 admits a metric of positive scalar curvature if and only if the
admits a metric of positive scalar curvature if and only if the 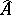 -genus of
-genus of  vanishes. This invariant takes values in
vanishes. This invariant takes values in 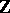 if
if 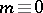 modulo
modulo 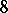 , in
, in 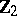 if
if 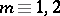 modulo
modulo 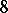 , in
, in 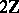 if
if 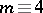 modulo
modulo 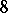 , and vanishes if
, and vanishes if 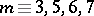 modulo
modulo 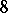 .
.
The situation is more complicated in the presence of a fundamental group 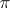 . Let
. Let 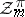 be the Grothendieck group of finitely generated
be the Grothendieck group of finitely generated 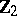 -graded modules over the Clifford algebra
-graded modules over the Clifford algebra 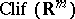 which have a
which have a 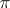 action commuting with the
action commuting with the 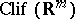 action. The inclusion
action. The inclusion 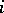 of
of  in
in 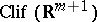 induces a dual pull-back
induces a dual pull-back 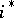 from
from 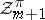 to
to 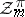 . The real
. The real 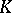 -theory groups of
-theory groups of  are given by:
are given by:
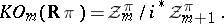 |
J. Rosenberg [a6] defined a 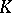 -theory-valued invariant
-theory-valued invariant 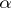 taking values in this group which generalizes the
taking values in this group which generalizes the 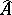 -genus. It was conjectured that this might provide a complete description of the obstruction to the existence of a metric of positive scalar curvature; this refined conjecture became known as the Gromov–Lawson–Rosenberg conjecture.
-genus. It was conjectured that this might provide a complete description of the obstruction to the existence of a metric of positive scalar curvature; this refined conjecture became known as the Gromov–Lawson–Rosenberg conjecture.
The conjecture was established for spherical space form groups [a1] and for finite Abelian groups of rank at most  and odd order [a8]. It has also been established for a (short) list of infinite groups, including free groups, free Abelian groups, and fundamental groups of orientable surfaces [a5]. S. Schick [a7] has shown that the conjecture, in the form due to J. Rosenberg, is false by exhibiting a compact spin manifold with fundamental group
and odd order [a8]. It has also been established for a (short) list of infinite groups, including free groups, free Abelian groups, and fundamental groups of orientable surfaces [a5]. S. Schick [a7] has shown that the conjecture, in the form due to J. Rosenberg, is false by exhibiting a compact spin manifold with fundamental group  which does not admit a metric of positive scalar curvature but for which the
which does not admit a metric of positive scalar curvature but for which the 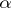 invariant vanishes. It is not known (1998) if the conjecture holds for finite fundamental groups.
invariant vanishes. It is not known (1998) if the conjecture holds for finite fundamental groups.
References
| [a1] | B. Botvinnik, P. Gilkey, S. Stolz, "The Gromov–Lawson–Rosenberg conjecture for groups with periodic cohomology" J. Diff. Geom. , 46 (1997) pp. 374–405 |
| [a2] | M. Gromov, H.B. Lawson, "Spin and scalar curvature in the presence of a fundamental group I" Ann. of Math. , 111 (1980) pp. 209–230 |
| [a3] | M. Gromov, H.B. Lawson, "The classification of simply connected manifolds of positive scalar curvature" Ann. of Math. , 111 (1980) pp. 423–434 |
| [a4] | A. Lichnerowicz, "Spineurs harmoniques" C.R. Acad. Sci. Paris , 257 (1963) pp. 7–9 |
| [a5] | J. Rosenberg, S. Stolz, "A "stable" version of the Gromov–Lawson conjecture" Contemp. Math. , 181 (1995) pp. 405–418 |
| [a6] | J. Rosenberg, "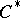 -algebras, positive scalar curvature, and the Novikov conjecture" Publ. Math. IHES , 58 (1983) pp. 197–212 -algebras, positive scalar curvature, and the Novikov conjecture" Publ. Math. IHES , 58 (1983) pp. 197–212 |
| [a7] | T. Schick, "A counterexample to the (unstable) Gromov–Lawson–Rosenberg conjecture" Topology , 37 (1998) pp. 1165–1168 |
| [a8] | R. Schultz, "Positive scalar curvature and odd order Abelian fundamental groups" Proc. Amer. Math. Soc. , 125 : 3 (1997) pp. 907–915 |
| [a9] | S. Stolz, "Simply connected manifolds of positive scalar curvature" Ann. of Math. , 136 (1992) pp. 511–540 |
Gromov-Lawson conjecture. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Gromov-Lawson_conjecture&oldid=11970