Difference between revisions of "Fejér summation method"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (moved Fejér summation method to Fejer summation method: ascii title) |
(No difference)
| |
Revision as of 18:52, 24 March 2012
A summation method of arithmetical averages (cf. Arithmetical averages, summation method of), applied to the summation of Fourier series. It was first applied by L. Fejér [1].
The Fourier series
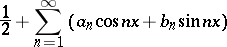 | (1) |
of a function 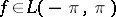 is summable by the Fejér summation method to a function
is summable by the Fejér summation method to a function  if
if
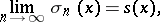 |
where
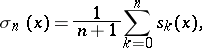 | (2) |
and the 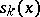 are the partial sums of (1).
are the partial sums of (1).
If  is a point of continuity of
is a point of continuity of 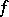 or a discontinuity of the first kind, then its Fourier series at that point is Fejér summable to
or a discontinuity of the first kind, then its Fourier series at that point is Fejér summable to 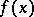 or to
or to 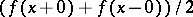 , respectively. If
, respectively. If 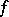 is continuous on some interval
is continuous on some interval 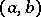 , then its Fourier series is uniformly Fejér summable on every segment
, then its Fourier series is uniformly Fejér summable on every segment  ; and if
; and if  is continuous everywhere, then the series is summable to
is continuous everywhere, then the series is summable to 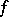 uniformly on
uniformly on 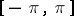 (Fejér's theorem).
(Fejér's theorem).
This result was strengthened by H. Lebesgue [2], who proved that for every summable function 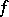 , its Fourier series is almost-everywhere Fejér summable to
, its Fourier series is almost-everywhere Fejér summable to 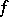 .
.
The function
 |
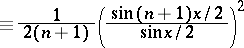 |
is called the Fejér kernel. It can be used to express the Fejér means (2) of 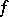 in the form
in the form
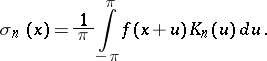 |
References
| [1] | L. Fejér, "Untersuchungen über Fouriersche Reihen" Math. Ann. , 58 (1903) pp. 51–69 |
| [2] | H. Lebesgue, "Recherches sur la convergence de séries de Fourier" Math. Ann. , 61 (1905) pp. 251–280 |
| [3] | N.K. [N.K. Bari] Bary, "A treatise on trigonometric series" , Pergamon (1964) (Translated from Russian) |
| [4] | A. Zygmund, "Trigonometric series" , 1–2 , Cambridge Univ. Press (1988) |
Comments
See also Cesàro summation methods.
Fejér summation method. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fej%C3%A9r_summation_method&oldid=18036