Difference between revisions of "Blaschke-Weyl formula"
From Encyclopedia of Mathematics
(Importing text file) |
Ulf Rehmann (talk | contribs) m (moved Blaschke–Weyl formula to Blaschke-Weyl formula: ascii title) |
(No difference)
| |
Revision as of 18:51, 24 March 2012
A variant of the Green formulas for the rotation field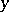 
of an infinitesimal deformation of a surface with position vector 
:
 |
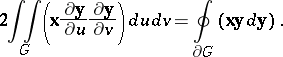The proof and the idea of applying the Blaschke–Weyl formula to demonstrate the rigidity of ovaloids is due to W. Blaschke [1] and to H. Weyl [2]. For other applications see [3]. The Herglotz formula is an analogue of the Blaschke–Weyl formula. The formula has been generalized to the case of infinitesimal deformations of surfaces in spaces of constant curvature.
References
| [1] | W. Blaschke, "Ein Beweis für die Unverbiegbarkeit geschlossener konvexer Flächen" Gött. Nachr. (1912) pp. 607–610 |
| [2] | H. Weyl, "Ueber die Starrheit der Eiflächen und konvexer Polyeder" Sitzungsber. Akad. Wiss. Berlin (1917) pp. 250–266 (Also: Gesammelte Abh., Vol. 1, Springer, 1968, pp. 646–662) |
| [3] | N.V. Efimov, "Qualitative problems in the theory of deformations of surfaces" Uspekhi Mat. Nauk , 3 : 2 (24) (1948) pp. 47–158 (In Russian) (Translated into German as book) |
| [4] | W. Blaschke, "Einführung in die Differentialgeometrie" , Springer (1950) |
How to Cite This Entry:
Blaschke-Weyl formula. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Blaschke-Weyl_formula&oldid=14686
Blaschke-Weyl formula. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Blaschke-Weyl_formula&oldid=14686
This article was adapted from an original article by M.I. Voitsekhovskii (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article