Difference between revisions of "Principal analytic fibration"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 30: | Line 30: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> M.F. Atiyah, "Vector bundles over an elliptic curve" ''Proc. London Math. Soc. (3)'' , '''7''' (1957) pp. 414–452 {{MR|0131423}} {{ZBL|0084.17305}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> L. Bungart, "On analytic fibre bundles - I. Holomorphic fibre bundles with infinite dimensional fibres" ''Topology'' , '''7''' (1968) pp. 55–68 {{MR|0222338}} {{MR|0201673}} {{ZBL|}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> J. Frenkel, "Cohomologie non Abélienne et espaces fibrés" ''Bull. Soc. Math. France'' , '''85''' (1957) pp. 135–220 {{MR|0098200}} {{ZBL|0082.37702}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> H. Grauert, "Analytische Faserungen über holomorph-vollständigen Räumen" ''Math. Ann.'' , '''135''' (1958) pp. 263–273 {{MR|0098199}} {{ZBL|0081.07401}} </TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> A. Grothendieck, "Sur la classification des fibres holomorphes sur la sphere de Riemann" ''Amer. J. Math.'' , '''79''' (1957) pp. 121–138 {{MR|0087176}} {{ZBL|0079.17001}} </TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> A. Ramanathan, "Stable principal bundles on a compact Riemann surface" ''Math. Ann.'' , '''213''' (1975) pp. 129–152 {{MR|0369747}} {{ZBL|0284.32019}} </TD></TR></table> |
| Line 38: | Line 38: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> A. van de Ven, "Twenty years of classifying algebraic vectorbundles" A. Beauville (ed.) , ''Journées de géometrie algébrique d'Angers'' , Sijthoff & Noordhoff (1980) pp. 3–20 {{MR|}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> R. Harshorne, "Four years of algebraic vectorbundles" A. Beauville (ed.) , ''Journées de géometrie algébrique d'Angers (1979)'' , Sijthoff & Noordhoff (1980) pp. 21–29 {{MR|}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> C. Okonek, M. Schneider, H. Spindler, "Vector bundles on complex projective spaces" , Birkhäuser (1980) {{MR|0561910}} {{ZBL|0438.32016}} </TD></TR></table> |
Revision as of 14:51, 24 March 2012
A locally trivial analytic fibration on the fibres of which the structure Lie group acts simply transitively and analytically. In other words, a principal analytic fibration is a quadruple 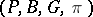 where
where  and
and  are analytic spaces (cf. Analytic space) over a field
are analytic spaces (cf. Analytic space) over a field  ;
;  is an analytic mapping;
is an analytic mapping;  is a Lie group over
is a Lie group over  analytically acting on
analytically acting on  from the right; and for each element of the base
from the right; and for each element of the base  there exist a neighbourhood
there exist a neighbourhood  and an analytic isomorphism
and an analytic isomorphism
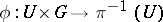 |
such that
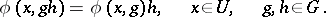 |
Each analytic vector bundle (cf. Vector bundle, analytic) 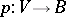 with
with  -dimensional fibre determines a principal analytic fibration with base
-dimensional fibre determines a principal analytic fibration with base  and group
and group 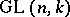 , whose fibre over a point
, whose fibre over a point 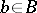 is the variety of all bases of the fibre
is the variety of all bases of the fibre 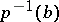 . This is a special case of a one-to-one correspondence between analytic fibrations with given fibre and structure group
. This is a special case of a one-to-one correspondence between analytic fibrations with given fibre and structure group 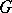 and the principal analytic fibrations associated with them. Other examples of principal analytic fibrations include the fibration
and the principal analytic fibrations associated with them. Other examples of principal analytic fibrations include the fibration 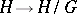 whose fibres are the left cosets of the Lie group
whose fibres are the left cosets of the Lie group 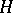 by a Lie subgroup
by a Lie subgroup 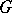 of it, and an analytic covering (here, the group of the covering is the structure group).
of it, and an analytic covering (here, the group of the covering is the structure group).
A principal analytic fibration can be defined by an open covering 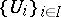 of its base
of its base 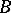 and transition functions, i.e. analytic mappings
and transition functions, i.e. analytic mappings
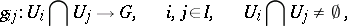 |
which satisfy the conditions
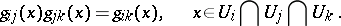 |
The transition functions form a one-dimensional cocycle with values in the sheaf 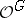 of germs of analytic mappings
of germs of analytic mappings 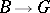 . This yields a one-to-one correspondence between the set of principal analytic fibrations with base
. This yields a one-to-one correspondence between the set of principal analytic fibrations with base  and group
and group 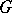 and the set of cohomology spaces
and the set of cohomology spaces 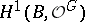 . The classification of the principal analytic fibrations with base
. The classification of the principal analytic fibrations with base 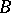 and structure group
and structure group 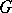 (in the case of a non-Abelian group
(in the case of a non-Abelian group 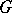 ) is a problem which has so far been solved in a number of cases only (cf. Deformation of an analytic structure, for the corresponding local moduli problem). The connection between this classification and the classification of principal topological fibrations is expressed by the natural mapping
) is a problem which has so far been solved in a number of cases only (cf. Deformation of an analytic structure, for the corresponding local moduli problem). The connection between this classification and the classification of principal topological fibrations is expressed by the natural mapping
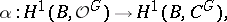 |
where  is the sheaf of germs of continuous mappings
is the sheaf of germs of continuous mappings 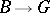 .
.
Let 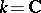 , and let
, and let 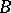 be a reduced Stein space; the mapping
be a reduced Stein space; the mapping 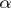 is then bijective, and the classification problem is reduced to a problem in homotopy theory [4]. In particular, any principal analytic fibration with a non-compact Riemann surface as base and with a connected structure group is trivial. The result of [4] was in fact obtained for the broader class of
is then bijective, and the classification problem is reduced to a problem in homotopy theory [4]. In particular, any principal analytic fibration with a non-compact Riemann surface as base and with a connected structure group is trivial. The result of [4] was in fact obtained for the broader class of 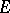 -principal fibrations, in the definition of which the group
-principal fibrations, in the definition of which the group  is replaced by some locally trivial analytic fibration
is replaced by some locally trivial analytic fibration 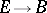 on complex Lie groups, acting fibre-wise on
on complex Lie groups, acting fibre-wise on  . This result has been generalized to the case when the structure group is a complex Banach Lie group [2]. If, on the other hand,
. This result has been generalized to the case when the structure group is a complex Banach Lie group [2]. If, on the other hand, 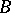 is a compact Riemann surface, then
is a compact Riemann surface, then 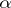 is surjective and not injective. In the general case
is surjective and not injective. In the general case 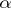 need not be either surjective nor injective. Sufficient cohomological conditions for
need not be either surjective nor injective. Sufficient cohomological conditions for 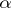 to be injective or surjective are known [3] for a connected solvable group
to be injective or surjective are known [3] for a connected solvable group 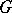 .
.
The case when 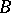 is a compact Riemann surface of genus
is a compact Riemann surface of genus 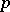 and
and 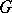 is a connected reductive algebraic group has been also studied. See [5] for the corresponding classification for
is a connected reductive algebraic group has been also studied. See [5] for the corresponding classification for 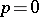 ; see [1] for the corresponding classification for
; see [1] for the corresponding classification for 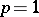 when
when  . In the case
. In the case  ,
, 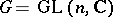 (cf. Vector bundle, algebraic) an important role is played by the concept of a stable vector bundle. This concept has been generalized [6] to the case of an arbitrary connected reductive group
(cf. Vector bundle, algebraic) an important role is played by the concept of a stable vector bundle. This concept has been generalized [6] to the case of an arbitrary connected reductive group 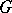 . The set of all stable principal fibrations of a given topological type on a compact Riemann surface has the natural structure of a connected normal analytic space. A partial classification of vector bundles over the complex projective space
. The set of all stable principal fibrations of a given topological type on a compact Riemann surface has the natural structure of a connected normal analytic space. A partial classification of vector bundles over the complex projective space 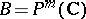 and over algebraic surfaces has also been obtained.
and over algebraic surfaces has also been obtained.
See Real-analytic space for real principal analytic fibrations (the case 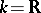 ).
).
References
| [1] | M.F. Atiyah, "Vector bundles over an elliptic curve" Proc. London Math. Soc. (3) , 7 (1957) pp. 414–452 MR0131423 Zbl 0084.17305 |
| [2] | L. Bungart, "On analytic fibre bundles - I. Holomorphic fibre bundles with infinite dimensional fibres" Topology , 7 (1968) pp. 55–68 MR0222338 MR0201673 |
| [3] | J. Frenkel, "Cohomologie non Abélienne et espaces fibrés" Bull. Soc. Math. France , 85 (1957) pp. 135–220 MR0098200 Zbl 0082.37702 |
| [4] | H. Grauert, "Analytische Faserungen über holomorph-vollständigen Räumen" Math. Ann. , 135 (1958) pp. 263–273 MR0098199 Zbl 0081.07401 |
| [5] | A. Grothendieck, "Sur la classification des fibres holomorphes sur la sphere de Riemann" Amer. J. Math. , 79 (1957) pp. 121–138 MR0087176 Zbl 0079.17001 |
| [6] | A. Ramanathan, "Stable principal bundles on a compact Riemann surface" Math. Ann. , 213 (1975) pp. 129–152 MR0369747 Zbl 0284.32019 |
Comments
For the partial classification of bundles over a complex projective space or an algebraic surface see [a1]–[a3].
References
| [a1] | A. van de Ven, "Twenty years of classifying algebraic vectorbundles" A. Beauville (ed.) , Journées de géometrie algébrique d'Angers , Sijthoff & Noordhoff (1980) pp. 3–20 |
| [a2] | R. Harshorne, "Four years of algebraic vectorbundles" A. Beauville (ed.) , Journées de géometrie algébrique d'Angers (1979) , Sijthoff & Noordhoff (1980) pp. 21–29 |
| [a3] | C. Okonek, M. Schneider, H. Spindler, "Vector bundles on complex projective spaces" , Birkhäuser (1980) MR0561910 Zbl 0438.32016 |
Principal analytic fibration. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Principal_analytic_fibration&oldid=17495