Difference between revisions of "Picard scheme"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 13: | Line 13: | ||
for any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072670/p07267026.png" />-scheme <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072670/p07267027.png" /> [[#References|[3]]]. In particular, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072670/p07267028.png" /> can be identified with the group of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072670/p07267029.png" />-rational points <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072670/p07267030.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072670/p07267031.png" /> if such exists. | for any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072670/p07267026.png" />-scheme <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072670/p07267027.png" /> [[#References|[3]]]. In particular, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072670/p07267028.png" /> can be identified with the group of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072670/p07267029.png" />-rational points <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072670/p07267030.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072670/p07267031.png" /> if such exists. | ||
| − | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072670/p07267032.png" /> is a projective morphism with geometrically-integral fibres, then the scheme <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072670/p07267033.png" /> exists and is a locally finitely representable separable group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072670/p07267034.png" />-scheme. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072670/p07267035.png" />, then the connected component of the unit, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072670/p07267036.png" />, of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072670/p07267037.png" /> is an algebraic <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072670/p07267038.png" />-scheme, and the corresponding reduced <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072670/p07267039.png" />-scheme <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072670/p07267040.png" /> is precisely the Picard variety <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072670/p07267041.png" /> [[#References|[4]]]. The nilpotent elements in the local rings of the scheme <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072670/p07267042.png" /> give much additional information on the Picard scheme and enable one to explain various | + | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072670/p07267032.png" /> is a projective morphism with geometrically-integral fibres, then the scheme <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072670/p07267033.png" /> exists and is a locally finitely representable separable group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072670/p07267034.png" />-scheme. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072670/p07267035.png" />, then the connected component of the unit, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072670/p07267036.png" />, of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072670/p07267037.png" /> is an algebraic <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072670/p07267038.png" />-scheme, and the corresponding reduced <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072670/p07267039.png" />-scheme <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072670/p07267040.png" /> is precisely the Picard variety <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072670/p07267041.png" /> [[#References|[4]]]. The nilpotent elements in the local rings of the scheme <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072670/p07267042.png" /> give much additional information on the Picard scheme and enable one to explain various "pathologies" in algebraic geometry over a field of characteristic <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072670/p07267043.png" />. On the other hand, over a field of characteristic 0 the scheme <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072670/p07267044.png" /> is always reduced [[#References|[6]]]. It is also known that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072670/p07267045.png" /> is a reduced scheme if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072670/p07267046.png" /> is a smooth algebraic surface and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072670/p07267047.png" /> [[#References|[5]]]. |
For any proper flat morphism <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072670/p07267048.png" /> (finitely representable if the base <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072670/p07267049.png" /> is Noetherian) for which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072670/p07267050.png" />, the functor <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072670/p07267051.png" /> is an algebraic space over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072670/p07267052.png" /> for any base-change morphism <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072670/p07267053.png" /> [[#References|[1]]]. In particular, the functor <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072670/p07267054.png" /> is representable if the ground scheme <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072670/p07267055.png" /> is the spectrum of a local Artinian ring. | For any proper flat morphism <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072670/p07267048.png" /> (finitely representable if the base <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072670/p07267049.png" /> is Noetherian) for which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072670/p07267050.png" />, the functor <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072670/p07267051.png" /> is an algebraic space over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072670/p07267052.png" /> for any base-change morphism <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072670/p07267053.png" /> [[#References|[1]]]. In particular, the functor <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072670/p07267054.png" /> is representable if the ground scheme <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072670/p07267055.png" /> is the spectrum of a local Artinian ring. | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> M. Artin, "Algebraization of formal moduli I" D.C. Spencer (ed.) S. Iyanaga (ed.) , ''Global analysis (papers in honor of K. Kodaira)'' , Univ. Tokyo Press (1969) pp. 21–72 {{MR|0260746}} {{ZBL|0205.50402}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> C. Chevalley, "Sur la théorie de la variété de Picard" ''Amer. J. Math.'' , '''82''' (1960) pp. 435–490 {{MR|0118723}} {{ZBL|0127.37701}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> A. Grothendieck, "Technique de déscente et théorèmes d'existence en géometrie algébrique. V. Les schémas de Picard. Théorèmes d'existence" ''Sém. Bourbaki'' , '''14''' (1962) pp. 232/01–232/19 {{MR|1611170}} {{ZBL|}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> A. Grothendieck, "Eléments de géomètrie algébrique. I Le langage des schémas" ''Publ. Math. IHES'' : 4 (1960) pp. 1–228 {{MR|0217083}} {{MR|0163908}} {{ZBL|0118.36206}} </TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> D. Mumford, "Lectures on curves on an algebraic surface" , Princeton Univ. Press (1966) {{MR|0209285}} {{ZBL|0187.42701}} </TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> F. Oort, "Algebraic group schemes in character zero are reduced" ''Invent. Math.'' , '''2''' : 1 (1966) pp. 79–80 {{MR|206005}} {{ZBL|}} </TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> I.V Dolgachev, "Abstract algebraic geometry" ''J. Soviet Math.'' , '''2''' : 3 (1974) pp. 264–303 ''Itogi Nauk. i Tekhn. Algebra. Topol. Geom.'' , '''10''' (1972) pp. 47–112 {{MR|}} {{ZBL|1068.14059}} </TD></TR></table> |
| Line 26: | Line 26: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> A. Grothendieck, "Fondements de la géométrie algébrique" , Secr. Math. Univ. Paris (1961/62) (Extracts Sem. Bourbaki 1957–1962) {{MR|1611235}} {{MR|1086880}} {{MR|0146040}} {{ZBL|0239.14002}} {{ZBL|0239.14001}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> A. Altman, S. Kleiman, "Compactification of the Picard scheme I" ''Adv. in Math.'' , '''35''' (1980) pp. 50–112 {{MR|}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> A. Altman, S. Kleiman, "Compactification of the Picard scheme II" ''Amer. J. Math.'' , '''101''' (1979) pp. 10–41 {{MR|}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> J.P. Murre, "On contravariant functors from the category of preschemes over a field into the category of abelian groups (with an application to the Picard functor)" ''Publ. Math. IHES'' , '''23''' (1964) pp. 581–619 {{MR|206011}} {{ZBL|0142.18402}} </TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> F. Oort, "Sur le schéma de Picard" ''Bull. Soc. Math. France'' , '''90''' (1962) pp. 1–14 {{MR|0138627}} {{ZBL|0123.13901}} </TD></TR></table> |
Revision as of 14:51, 24 March 2012
A natural generalization of the concept of the Picard variety 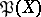 for a smooth algebraic variety
for a smooth algebraic variety 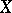 within the framework of the theory of schemes. To define the Picard scheme for an arbitrary
within the framework of the theory of schemes. To define the Picard scheme for an arbitrary 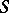 -scheme
-scheme 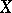 one considers the relative Picard functor
one considers the relative Picard functor 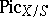 in the category
in the category 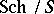 of schemes over the scheme
of schemes over the scheme 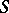 . The value of this functor on an
. The value of this functor on an 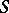 -scheme
-scheme 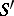 is the group
is the group
 |
where 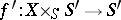 is the base-change morphism and
is the base-change morphism and 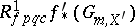 is the sheaf in the Grothendieck topology
is the sheaf in the Grothendieck topology  of strictly-flat quasi-compact morphisms associated with the pre-sheaf
of strictly-flat quasi-compact morphisms associated with the pre-sheaf
 |
and 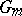 denotes the standard multiplicative group sheaf. If the Picard functor
denotes the standard multiplicative group sheaf. If the Picard functor 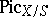 is representable on
is representable on  , then the
, then the 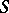 -scheme representing it is called the relative Picard scheme for the
-scheme representing it is called the relative Picard scheme for the 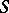 -scheme
-scheme 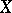 and is denoted by
and is denoted by 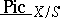 . If
. If  is an algebraic scheme over a certain field
is an algebraic scheme over a certain field 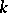 having a rational
having a rational 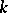 -point, then
-point, then
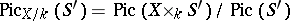 |
for any 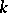 -scheme
-scheme 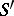 [3]. In particular,
[3]. In particular, 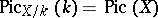 can be identified with the group of
can be identified with the group of 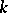 -rational points
-rational points 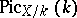 of
of 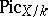 if such exists.
if such exists.
If  is a projective morphism with geometrically-integral fibres, then the scheme
is a projective morphism with geometrically-integral fibres, then the scheme  exists and is a locally finitely representable separable group
exists and is a locally finitely representable separable group 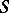 -scheme. If
-scheme. If 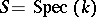 , then the connected component of the unit,
, then the connected component of the unit,  , of
, of 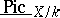 is an algebraic
is an algebraic  -scheme, and the corresponding reduced
-scheme, and the corresponding reduced 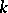 -scheme
-scheme 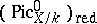 is precisely the Picard variety
is precisely the Picard variety 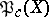 [4]. The nilpotent elements in the local rings of the scheme
[4]. The nilpotent elements in the local rings of the scheme  give much additional information on the Picard scheme and enable one to explain various "pathologies" in algebraic geometry over a field of characteristic
give much additional information on the Picard scheme and enable one to explain various "pathologies" in algebraic geometry over a field of characteristic 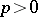 . On the other hand, over a field of characteristic 0 the scheme
. On the other hand, over a field of characteristic 0 the scheme 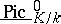 is always reduced [6]. It is also known that
is always reduced [6]. It is also known that 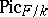 is a reduced scheme if
is a reduced scheme if 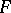 is a smooth algebraic surface and
is a smooth algebraic surface and 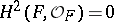 [5].
[5].
For any proper flat morphism 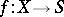 (finitely representable if the base
(finitely representable if the base 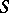 is Noetherian) for which
is Noetherian) for which 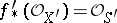 , the functor
, the functor 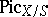 is an algebraic space over
is an algebraic space over 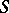 for any base-change morphism
for any base-change morphism 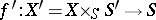 [1]. In particular, the functor
[1]. In particular, the functor 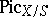 is representable if the ground scheme
is representable if the ground scheme 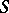 is the spectrum of a local Artinian ring.
is the spectrum of a local Artinian ring.
References
| [1] | M. Artin, "Algebraization of formal moduli I" D.C. Spencer (ed.) S. Iyanaga (ed.) , Global analysis (papers in honor of K. Kodaira) , Univ. Tokyo Press (1969) pp. 21–72 MR0260746 Zbl 0205.50402 |
| [2] | C. Chevalley, "Sur la théorie de la variété de Picard" Amer. J. Math. , 82 (1960) pp. 435–490 MR0118723 Zbl 0127.37701 |
| [3] | A. Grothendieck, "Technique de déscente et théorèmes d'existence en géometrie algébrique. V. Les schémas de Picard. Théorèmes d'existence" Sém. Bourbaki , 14 (1962) pp. 232/01–232/19 MR1611170 |
| [4] | A. Grothendieck, "Eléments de géomètrie algébrique. I Le langage des schémas" Publ. Math. IHES : 4 (1960) pp. 1–228 MR0217083 MR0163908 Zbl 0118.36206 |
| [5] | D. Mumford, "Lectures on curves on an algebraic surface" , Princeton Univ. Press (1966) MR0209285 Zbl 0187.42701 |
| [6] | F. Oort, "Algebraic group schemes in character zero are reduced" Invent. Math. , 2 : 1 (1966) pp. 79–80 MR206005 |
| [7] | I.V Dolgachev, "Abstract algebraic geometry" J. Soviet Math. , 2 : 3 (1974) pp. 264–303 Itogi Nauk. i Tekhn. Algebra. Topol. Geom. , 10 (1972) pp. 47–112 Zbl 1068.14059 |
Comments
The standard multiplicative sheaf over a scheme 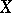 assigns to an affine open set
assigns to an affine open set  in
in  the group
the group 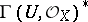 of units of
of units of 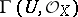 .
.
References
| [a1] | A. Grothendieck, "Fondements de la géométrie algébrique" , Secr. Math. Univ. Paris (1961/62) (Extracts Sem. Bourbaki 1957–1962) MR1611235 MR1086880 MR0146040 Zbl 0239.14002 Zbl 0239.14001 |
| [a2] | A. Altman, S. Kleiman, "Compactification of the Picard scheme I" Adv. in Math. , 35 (1980) pp. 50–112 |
| [a3] | A. Altman, S. Kleiman, "Compactification of the Picard scheme II" Amer. J. Math. , 101 (1979) pp. 10–41 |
| [a4] | J.P. Murre, "On contravariant functors from the category of preschemes over a field into the category of abelian groups (with an application to the Picard functor)" Publ. Math. IHES , 23 (1964) pp. 581–619 MR206011 Zbl 0142.18402 |
| [a5] | F. Oort, "Sur le schéma de Picard" Bull. Soc. Math. France , 90 (1962) pp. 1–14 MR0138627 Zbl 0123.13901 |
Picard scheme. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Picard_scheme&oldid=15715