Difference between revisions of "Comitant"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 28: | Line 28: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> G.B. Gurevich, "Foundations of the theory of algebraic invariants" , Noordhoff (1964) (Translated from Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> D. Mumford, "Geometric invariant theory" , Springer (1965)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> J.A. Dieudonné, "La géométrie des groups classiques" , Springer (1955)</TD></TR></table> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> G.B. Gurevich, "Foundations of the theory of algebraic invariants" , Noordhoff (1964) (Translated from Russian) {{MR|0183733}} {{ZBL|0128.24601}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> D. Mumford, "Geometric invariant theory" , Springer (1965) {{MR|0214602}} {{ZBL|0147.39304}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> J.A. Dieudonné, "La géométrie des groups classiques" , Springer (1955) {{MR|}} {{ZBL|0221.20056}} </TD></TR></table> |
Revision as of 10:02, 24 March 2012
concomitant of a group 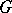 acting on sets
acting on sets 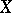 and
and 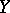
A mapping 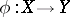 such that
such that
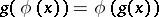 |
for any 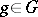 ,
, 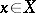 . In this case one also says that
. In this case one also says that 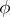 commutes with the action of
commutes with the action of 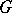 , or that
, or that 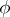 is an equivariant mapping. If
is an equivariant mapping. If  acts on every set of a family
acts on every set of a family 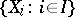 , then a comitant
, then a comitant 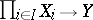 is called a simultaneous comitant of
is called a simultaneous comitant of 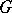 .
.
The notion of a comitant originates from the classical theory of invariants (cf. Invariants, theory of) in which, however, a comitant is understood in a narrower sense: 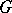 is the general linear group of some finite-dimensional vector space
is the general linear group of some finite-dimensional vector space  ,
, 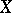 and
and 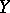 are tensor spaces on
are tensor spaces on 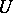 of specified (generally distinct) types, on which
of specified (generally distinct) types, on which 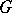 acts in the natural way, while
acts in the natural way, while 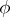 is an equivariant polynomial mapping from
is an equivariant polynomial mapping from 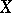 into
into  . If, in addition,
. If, in addition, 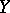 is a space of covariant tensors, then the comitant is called a covariant of
is a space of covariant tensors, then the comitant is called a covariant of 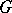 , while if
, while if 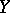 is a space of contravariant tensors, the comitant is called a contravariant of
is a space of contravariant tensors, the comitant is called a contravariant of 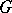 .
.
Example. Let 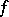 be a binary cubic form in the variables
be a binary cubic form in the variables  and
and 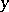 :
:
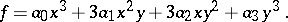 |
Its coefficients are the coordinates of a covariant symmetric tensor. The coefficients of the Hessian form of 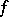 , that is, of the form
, that is, of the form
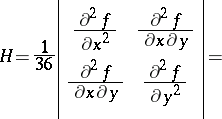 |
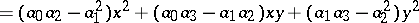 |
are also the coefficients of a covariant symmetric tensor, while the mapping
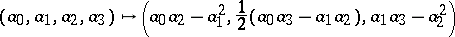 |
of the corresponding tensor spaces is a comitant (the so-called comitant of the form 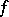 ). The Hessian of an arbitrary form can similarly be defined; this also provides an example of a comitant (see Covariant).
). The Hessian of an arbitrary form can similarly be defined; this also provides an example of a comitant (see Covariant).
In the modern geometric theory of invariants, by a comitant one often means any equivariant morphism 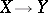 , where
, where 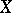 and
and 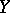 are algebraic varieties endowed with a regular action of an algebraic group
are algebraic varieties endowed with a regular action of an algebraic group 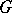 . If
. If 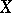 and
and 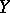 are affine, then giving a comitant is equivalent to giving a homomorphism
are affine, then giving a comitant is equivalent to giving a homomorphism 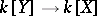 of
of  -modules of regular functions on the varieties
-modules of regular functions on the varieties 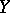 and
and 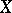 , respectively (where
, respectively (where 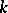 is the ground field).
is the ground field).
References
| [1] | G.B. Gurevich, "Foundations of the theory of algebraic invariants" , Noordhoff (1964) (Translated from Russian) MR0183733 Zbl 0128.24601 |
| [2] | D. Mumford, "Geometric invariant theory" , Springer (1965) MR0214602 Zbl 0147.39304 |
| [3] | J.A. Dieudonné, "La géométrie des groups classiques" , Springer (1955) Zbl 0221.20056 |
Comitant. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Comitant&oldid=15732