Difference between revisions of "Injection"
From Encyclopedia of Mathematics
(Importing text file) |
m |
||
| Line 1: | Line 1: | ||
''injective mapping, of a set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i051/i051200/i0512001.png" /> into a set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i051/i051200/i0512002.png" />'' | ''injective mapping, of a set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i051/i051200/i0512001.png" /> into a set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i051/i051200/i0512002.png" />'' | ||
| − | A mapping | + | A mapping $ f : A \to B $ under which different elements of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i051/i051200/i0512004.png" /> have different images in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i051/i051200/i0512005.png" />. An injection is also called an imbedding (or inclusion) of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i051/i051200/i0512006.png" /> into <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i051/i051200/i0512007.png" />. |
Revision as of 23:36, 15 February 2012
injective mapping, of a set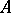 
into a set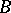 
A mapping $ f : A \to B $ under which different elements of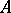 
have different images in 
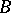. An injection is also called an imbedding (or inclusion) of 
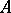into 
.
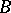Comments
In category theory, a morphism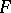 
is called injective if for all morphisms 
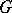and 
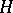: If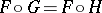 
, then 
.
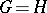How to Cite This Entry:
Injection. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Injection&oldid=11558
Injection. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Injection&oldid=11558
This article was adapted from an original article by O.A. Ivanova (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article