|
|
| Line 1: |
Line 1: |
| − | ''crossed product, of a group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027120/c0271201.png" /> and a ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027120/c0271202.png" />'' | + | ''crossed product, of a group $G$ and a ring $K$'' |
| | | | |
| − | An associative ring defined as follows. Suppose one is given a mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027120/c0271203.png" /> of a group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027120/c0271204.png" /> into the isomorphism group of an associative ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027120/c0271205.png" /> with an identity, and a family | + | An associative ring defined as follows. Suppose one is given a mapping $\sigma$ of a group $G$ into the isomorphism group of an associative ring $K$ with identity, and a family |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027120/c0271206.png" /></td> </tr></table>
| + | $$ \rho = \{ \rho_{g,h} | g,h \in G\} $$ |
| | | | |
| − | of invertible elements of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027120/c0271207.png" />, satisfying the conditions | + | of invertible elements of $K$, satisfying the conditions |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027120/c0271208.png" /></td> </tr></table>
| + | $$ \rho_{g_1,g_2}\rho_{g_1g_2,g_3} = \rho^{\sigma(g_1)}_{g_2,g_3}\rho_{g_1,g_2g_3} $$ |
| | + | $$ \alpha^{\sigma(g_2)\sigma(g_1)} = \rho_{g_1,g_2}\alpha^{\sigma(g_1g_2)}\rho^{-1}_{g_1,g_2} $$ |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027120/c0271209.png" /></td> </tr></table>
| + | for all $\alpha\in K$ and $g_1,g_2,g_3\in G$. The family $\rho$ is called a factor system. Then the cross product of $G$ and $K$ with respect to the factor system $\rho$ and the mapping $\sigma$ is the set of all formal finite sums of the form |
| | | | |
| − | for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027120/c02712010.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027120/c02712011.png" />. The family <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027120/c02712012.png" /> is called a factor system. Then the cross product of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027120/c02712013.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027120/c02712014.png" /> with respect to the factor system <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027120/c02712015.png" /> and the mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027120/c02712016.png" /> is the set of all formal finite sums of the form
| + | $$ \sum_{g\in G} \alpha_g t_g $$ |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027120/c02712017.png" /></td> </tr></table>
| + | where $\alpha_g \in K$ and the $t_g$ are symbols uniquely assigned to every element $g\in G$, with binary operations defined by |
| | | | |
| − | (where the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027120/c02712018.png" /> are symbols uniquely assigned to every element <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027120/c02712019.png" />), with binary operations defined by | + | $$ \sum_{g\in G} \alpha_g t_g + \sum_{g\in G} \beta_g t_g = \sum_{g\in G} (\alpha_g+\beta_g)t_g,$$ |
| | + | $$ \left(\sum_{g\in G}\alpha_gt_g\right) \left(\sum_{g\in G}\beta_gt_g\right) = \sum_{g\in G} \left(\sum_{h_1h_2=g}\alpha_{h_1}\beta^{\sigma(h_1)}_{h_2}\rho_{h_1,h_2}\right) t_g $$ |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027120/c02712020.png" /></td> </tr></table>
| + | This ring is denoted by $K(G, \rho, \sigma)$; the elements $t_g$ form a $K$-basis for the ring. |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027120/c02712021.png" /></td> </tr></table>
| + | If $\sigma$ maps $G$ onto the identity automorphism of $K$, then $K(G, \rho)$ is called a twisted or crossed group ring, and if, in addition, $\rho_{g,h}=1$ for all $g,h\in G$, then $K(G,\rho,\sigma)$ is the group ring of $G$ over $K$ (see [[Group algebra|Group algebra]]). |
| | | | |
| − | This ring is denoted by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027120/c02712022.png" />; the elements <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027120/c02712023.png" /> form a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027120/c02712024.png" />-basis of it.
| + | Let $K$ be a field and $\sigma$ a monomorphism. Then $K(G,\rho,\sigma)$ is a simple ring, being the cross product of the field with its Galois group. |
| − | | |
| − | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027120/c02712025.png" /> maps <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027120/c02712026.png" /> onto the identity automorphism of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027120/c02712027.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027120/c02712028.png" /> is called a twisted or crossed group ring, and if, in addition, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027120/c02712029.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027120/c02712030.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027120/c02712031.png" /> is the group ring of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027120/c02712032.png" /> over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027120/c02712033.png" /> (see [[Group algebra|Group algebra]]).
| |
| − | | |
| − | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027120/c02712034.png" /> be a field and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027120/c02712035.png" /> a monomorphism. Then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027120/c02712036.png" /> is a simple ring, being the cross product of the field with its Galois group. | |
| | | | |
| | ====References==== | | ====References==== |
Revision as of 03:09, 1 February 2012
crossed product, of a group $G$ and a ring $K$
An associative ring defined as follows. Suppose one is given a mapping $\sigma$ of a group $G$ into the isomorphism group of an associative ring $K$ with identity, and a family
$$ \rho = \{ \rho_{g,h} | g,h \in G\} $$
of invertible elements of $K$, satisfying the conditions
$$ \rho_{g_1,g_2}\rho_{g_1g_2,g_3} = \rho^{\sigma(g_1)}_{g_2,g_3}\rho_{g_1,g_2g_3} $$
$$ \alpha^{\sigma(g_2)\sigma(g_1)} = \rho_{g_1,g_2}\alpha^{\sigma(g_1g_2)}\rho^{-1}_{g_1,g_2} $$
for all $\alpha\in K$ and $g_1,g_2,g_3\in G$. The family $\rho$ is called a factor system. Then the cross product of $G$ and $K$ with respect to the factor system $\rho$ and the mapping $\sigma$ is the set of all formal finite sums of the form
$$ \sum_{g\in G} \alpha_g t_g $$
where $\alpha_g \in K$ and the $t_g$ are symbols uniquely assigned to every element $g\in G$, with binary operations defined by
$$ \sum_{g\in G} \alpha_g t_g + \sum_{g\in G} \beta_g t_g = \sum_{g\in G} (\alpha_g+\beta_g)t_g,$$
$$ \left(\sum_{g\in G}\alpha_gt_g\right) \left(\sum_{g\in G}\beta_gt_g\right) = \sum_{g\in G} \left(\sum_{h_1h_2=g}\alpha_{h_1}\beta^{\sigma(h_1)}_{h_2}\rho_{h_1,h_2}\right) t_g $$
This ring is denoted by $K(G, \rho, \sigma)$; the elements $t_g$ form a $K$-basis for the ring.
If $\sigma$ maps $G$ onto the identity automorphism of $K$, then $K(G, \rho)$ is called a twisted or crossed group ring, and if, in addition, $\rho_{g,h}=1$ for all $g,h\in G$, then $K(G,\rho,\sigma)$ is the group ring of $G$ over $K$ (see Group algebra).
Let $K$ be a field and $\sigma$ a monomorphism. Then $K(G,\rho,\sigma)$ is a simple ring, being the cross product of the field with its Galois group.
References
| [1] | S.K. Sehgal, "Topics in group rings" , M. Dekker (1978) |
| [2] | A.A. Bovdi, "Cross products of semi-groups and rings" Sibirsk. Mat. Zh. , 4 (1963) pp. 481–499 (In Russian) |
| [3] | A.E. Zalesskii, A.V. Mikhalev, "Group rings" J. Soviet Math. , 4 (1975) pp. 1–74 Itogi Nauk. i Tekhn. Sovrem. Probl. Mat. , 2 (1973) pp. 5–118 |
| [4] | D.S. Passman, "The algebraic structure of group rings" , Wiley (1977) |
In the defining relations for a factor system above  , e.g., of course stands for the result of applying the automorphism
, e.g., of course stands for the result of applying the automorphism  to the element
to the element  . If
. If  for all
for all  , then one obtains the skew group ring
, then one obtains the skew group ring  . Cross products arise naturally when dealing with extensions. Indeed, let
. Cross products arise naturally when dealing with extensions. Indeed, let  be a normal subgroup of
be a normal subgroup of 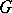 . Choose a set of representatives
. Choose a set of representatives  of
of  in
in  . Then every
. Then every 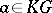 , the group algebra of
, the group algebra of 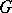 , can be written as a unique sum
, can be written as a unique sum  ,
, 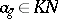 . Now write
. Now write
Then the  define a factor system (for the group
define a factor system (for the group 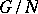 and the ring
and the ring  relative to the set of automorphisms
relative to the set of automorphisms  ) and
) and
Up to Brauer equivalence every central simple algebra is a cross product, but not every division algebra is isomorphic to a cross product. Two algebras  over
over  are Brauer equivalent if
are Brauer equivalent if 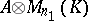 is isomorphic to
is isomorphic to  for suitable
for suitable 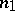 and
and  . Here
. Here 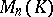 is the algebra of
is the algebra of 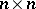 matrices over
matrices over  . Cf. also Brauer group.
. Cf. also Brauer group.
How to Cite This Entry:
Cross product. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cross_product&oldid=16831
This article was adapted from an original article by A.A. Bovdi (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098.
See original article , e.g., of course stands for the result of applying the automorphism
, e.g., of course stands for the result of applying the automorphism  to the element
to the element  . If
. If  for all
for all  , then one obtains the skew group ring
, then one obtains the skew group ring  . Cross products arise naturally when dealing with extensions. Indeed, let
. Cross products arise naturally when dealing with extensions. Indeed, let  be a normal subgroup of
be a normal subgroup of 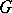 . Choose a set of representatives
. Choose a set of representatives  of
of  in
in  . Then every
. Then every 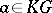 , the group algebra of
, the group algebra of 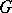 , can be written as a unique sum
, can be written as a unique sum  ,
, 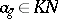 . Now write
. Now write
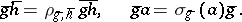
 define a factor system (for the group
define a factor system (for the group 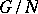 and the ring
and the ring  relative to the set of automorphisms
relative to the set of automorphisms  ) and
) and
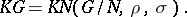
 over
over  are Brauer equivalent if
are Brauer equivalent if 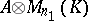 is isomorphic to
is isomorphic to  for suitable
for suitable 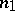 and
and  . Here
. Here 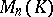 is the algebra of
is the algebra of 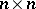 matrices over
matrices over  . Cf. also Brauer group.
. Cf. also Brauer group.