Difference between revisions of "Wold decomposition"
(Importing text file) |
(latex details) |
||
| (2 intermediate revisions by one other user not shown) | |||
| Line 1: | Line 1: | ||
| + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, | ||
| + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
| + | was used. | ||
| + | If the TeX and formula formatting is correct and if all png images have been replaced by TeX code, please remove this message and the {{TEX|semi-auto}} category. | ||
| + | |||
| + | Out of 72 formulas, 71 were replaced by TEX code.--> | ||
| + | |||
| + | {{TEX|semi-auto}}{{TEX|part}} | ||
A decomposition introduced by H. Wold in 1938 (see [[#References|[a7]]]); see also [[#References|[a5]]], [[#References|[a8]]]. Standard references include [[#References|[a6]]], [[#References|[a3]]]. | A decomposition introduced by H. Wold in 1938 (see [[#References|[a7]]]); see also [[#References|[a5]]], [[#References|[a8]]]. Standard references include [[#References|[a6]]], [[#References|[a3]]]. | ||
| − | The Wold decomposition of a (weakly) [[Stationary stochastic process|stationary stochastic process]] | + | The Wold decomposition of a (weakly) [[Stationary stochastic process|stationary stochastic process]] $\{ x _ { t } : t \in \mathbf{Z} \}$, $x _ { t } : \Omega \rightarrow \mathbf{R} ^ { n }$, provides interesting insights in the structure of such processes and, in particular, is an important tool for forecasting (from an infinite past). |
The main result can be summarized as: | The main result can be summarized as: | ||
| − | 1) Every (weakly) stationary process | + | 1) Every (weakly) stationary process $\{ x _ { t } : t \in \mathbf{Z} \}$ can uniquely be decomposed as |
| − | + | \begin{equation*} x _ { t } = y _ { t } + z _ { t }, \end{equation*} | |
| − | where the stationary processes | + | where the stationary processes $( y _ { t } )$ and $( z _ { t } )$ are obtained by causal linear transformations of $( x _ { t } )$ (where "causal" means that, e.g. $y _ { t }$, only depends on $x _ { s }$, $s \leq t$), $( y _ { t } )$ and $( z _ { t } )$ are mutually uncorrelated, $( y _ { t } )$ is linearly regular (i.e. the best linear least squares predictors converge to zero, if the forecasting horizon tends to infinity) and $( z _ { t } )$ is linearly singular (i.e. the prediction errors for the best linear least squares predictors are zero). |
| − | 2) Every linearly regular process | + | 2) Every linearly regular process $( y _ { t } )$ can be represented as |
| − | + | \begin{equation} \tag{a1} y _ { t } = \sum _ { j = 0 } ^ { \infty } K _ { j } \varepsilon _ { t - j }, \end{equation} | |
| − | + | \begin{equation*} K _ { j } \in {\bf R} ^ { n \times n } , K _ { 0 } = I , \sum _ { j = 0 } ^ { \infty } \| K _ { j } \| ^ { 2 } < \infty , \end{equation*} | |
| − | where | + | where $\varepsilon _ { t }$ is [[White noise|white noise]] (i.e. $\mathsf{E} \varepsilon _ { t } = 0$, $\mathsf{E} \varepsilon _ { t } \varepsilon _ { s } ^ { \prime } = \delta _ { s t } \Sigma$) and $\varepsilon _ { t }$ is obtained by a causal linear transformation of $( y _ { t } )$. |
| − | The construction behind the Wold decomposition in the [[Hilbert space|Hilbert space]] | + | The construction behind the Wold decomposition in the [[Hilbert space|Hilbert space]] $H$ spanned by the one-dimensional process variables $x _ { t } ^ { ( i ) }$ is as follows: If $H _ { x } ( t )$ denotes the subspace spanned by $\left\{ x _ { s } ^ { ( i ) } : s \leq t ,\, i = 1 , \dots , n \right\}$, then $z _ { t } ^ { ( i ) }$ is obtained from projecting $x _ { t } ^ { ( i ) }$ on the space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w130/w130170/w13017029.png"/>, and $\varepsilon _ { t } ^ { (i) }$ is obtained as the perpendicular by projecting $y _ { t } ^ { ( i ) }$ on the space $H _ { y } ( t - 1 )$ spanned by $\left\{ y _ { s } ^ { ( i ) } : s < t ,\; i = 1 , \dots , n \right\}$. Thus $\varepsilon _ { t }$ is the innovation and the one-step-ahead prediction error for $y _ { t }$ as well as for $x _ { t }$. |
| − | The implications of the above-mentioned results for (linear least squares) prediction are straightforward: Since | + | The implications of the above-mentioned results for (linear least squares) prediction are straightforward: Since $( y _ { t } )$ and $( z _ { t } )$ are orthogonal and since $H _ { x } ( t )$ is the direct sum of $H _ { y } ( t )$ and $H _ { z } ( t )$, the prediction problem can be solved for the linearly regular and the linearly singular part separately, and for a linearly regular process $( y _ { t } )$, $H _ { y } ( t ) = H _ { \epsilon } ( t )$ implies that the best linear least squares $r$-step ahead predictor for $y _ { t+r} $ is given by |
| − | + | \begin{equation*} \hat { y } _ { t , r } = \sum _ { j = r } ^ { \infty } K _ { j } \varepsilon _ { t + r - j } \end{equation*} | |
and thus the prediction error is | and thus the prediction error is | ||
| − | + | \begin{equation*} y _ { t + r } - \hat { y } _ { t , r } = \sum _ { j = 0 } ^ { r - 1 } K _ { j } \varepsilon _ { t + r - j }. \end{equation*} | |
Thus, when the representation (a1) is available, the prediction problem for a linearly regular process can be solved. | Thus, when the representation (a1) is available, the prediction problem for a linearly regular process can be solved. | ||
| − | The next problem is to obtain (a1) from the second moments of | + | The next problem is to obtain (a1) from the second moments of $( y _ { t } )$ (cf. also [[Moment|Moment]]). The problem of determining the coefficients $K_j$ of the Wold representation (a1) (or, equivalently, of determining the corresponding transfer function $k ( e ^ { - i \lambda } ) = \sum _ { j = 0 } ^ { \infty } K _ { j } e ^ { - i \lambda j }$) from the [[Spectral density|spectral density]] |
| − | + | \begin{equation} \tag{a2} f ( \lambda ) = ( 2 \pi ) ^ { - 1 } k ( e ^ { - i \lambda } ) \Sigma k ^ { * } ( e ^ { - i \lambda } ), \end{equation} | |
| − | (where the | + | (where the $*$ denotes the conjugate transpose) of a linearly regular process $( y _ { t } )$, is called the spectral factorization problem. The following result holds: |
| − | 3) A stationary process | + | 3) A stationary process $( y _ { t } )$ with a spectral density $f$, which is non-singular $\lambda$-a.e., is linearly regular if and only if |
| − | + | \begin{equation*} \int _ { - \pi } ^ { \pi } \operatorname { log } \operatorname { det } f ( \lambda ) d \lambda > - \infty. \end{equation*} | |
| − | In this case the factorization | + | In this case the factorization $( k , \Sigma )$ in (a2) corresponding to the Wold representation (a1) satisfies the relation |
| − | + | \begin{equation*} \operatorname { det } \Sigma = \operatorname { exp } \left\{ ( 2 \pi ) ^ { - 1 } \int _ { - \pi } ^ { \pi } \operatorname { log } \operatorname { det } 2 \pi f ( \lambda ) d \lambda \right\}. \end{equation*} | |
The most important special case is that of rational spectral densities; for such one has (see e.g. [[#References|[a4]]]): | The most important special case is that of rational spectral densities; for such one has (see e.g. [[#References|[a4]]]): | ||
| − | 4) Any rational and | + | 4) Any rational and $\lambda$-a.e. non-singular spectral density $f$ can be uniquely factorized, such that $k ( z )$ (the extension of $k ( e ^ { - i \lambda } )$ to $\mathbf{C}$) is rational, analytic within a circle containing the closed unit disc, $\operatorname { det } k ( z ) \neq 0$, $| z | < 1$, $k ( 0 ) = I$ (and thus corresponds to the Wold representation (a1)), and $\Sigma > 0$. Then (a1) is the solution of a stable and miniphase ARMA or a (linear) finite-dimensional state space system. |
Evidently, the Wold representation (a1) relates stationary processes to linear systems with white noise inputs. Actually, Wold introduced (a1) as a joint representation for AR and MA systems (cf. also [[Mixed autoregressive moving-average process|Mixed autoregressive moving-average process]]). | Evidently, the Wold representation (a1) relates stationary processes to linear systems with white noise inputs. Actually, Wold introduced (a1) as a joint representation for AR and MA systems (cf. also [[Mixed autoregressive moving-average process|Mixed autoregressive moving-average process]]). | ||
| − | The Wold representation is used, e.g., for the construction of the state space of a linearly regular process and the construction of state space representations, see [[#References|[a1]]], [[#References|[a4]]]. As mentioned already, the case of rational transfer functions corresponding to stable and miniphase ARMA or (finite-dimensional) state space systems is by far the most important one. In this case there is a wide class of identification procedures available, which also give estimates of the coefficients | + | The Wold representation is used, e.g., for the construction of the state space of a linearly regular process and the construction of state space representations, see [[#References|[a1]]], [[#References|[a4]]]. As mentioned already, the case of rational transfer functions corresponding to stable and miniphase ARMA or (finite-dimensional) state space systems is by far the most important one. In this case there is a wide class of identification procedures available, which also give estimates of the coefficients $K_j$ from finite data $y _ { 1 } , \dots , y _ { T }$ (see e.g. [[#References|[a4]]]). |
| − | Another case is that of stationary long memory processes (see e.g. [[#References|[a2]]]). In this case, in (a1), | + | Another case is that of stationary long memory processes (see e.g. [[#References|[a2]]]). In this case, in (a1), $\| \sum _ { j = 0 } ^ { \infty } K _ { j } \| ^ { 2 } = \infty$, so that $f$ is infinity at frequency zero, which causes the long memory effect. Models of this kind, in particular so-called ARFIMA models, have attracted considerable attention in modern econometrics. |
====References==== | ====References==== | ||
| − | <table>< | + | <table> |
| + | <tr><td valign="top">[a1]</td> <td valign="top"> H. Akaike, "Stochastic theory of minimal realizations" ''IEEE Trans. Autom. Control'' , '''AC-19''' (1974) pp. 667–674</td></tr><tr><td valign="top">[a2]</td> <td valign="top"> C.W.J. Granger, R. Joyeux, "An introduction to long memory time series models and fractional differencing" ''J. Time Ser. Anal.'' , '''1''' (1980) pp. 15–39</td></tr><tr><td valign="top">[a3]</td> <td valign="top"> E.J. Hannan, "Multiple time series" , Wiley (1970)</td></tr><tr><td valign="top">[a4]</td> <td valign="top"> E.J. Hannan, M. Deistler, "The statistical theory of linear systems" , Wiley (1988)</td></tr><tr><td valign="top">[a5]</td> <td valign="top"> A.N. Kolmogorov, "Stationary sequences in Hilbert space" ''Bull. Moscow State Univ.'' , '''2''' : 6 (1941) pp. 1–40</td></tr><tr><td valign="top">[a6]</td> <td valign="top"> Y.A. Rozanov, "Stationary random processes" , Holden Day (1967)</td></tr><tr><td valign="top">[a7]</td> <td valign="top"> H. Wold, "Study in the analysis of stationary time series" , Almqvist and Wiksell (1954) (Edition: Second)</td></tr><tr><td valign="top">[a8]</td> <td valign="top"> V.N. Zasukhin, "On the theory of multidimensional stationary processes" ''Dokl. Akad. Nauk SSSR'' , '''33''' (1941) pp. 435–437</td></tr> | ||
| + | </table> | ||
Latest revision as of 09:30, 3 February 2024
A decomposition introduced by H. Wold in 1938 (see [a7]); see also [a5], [a8]. Standard references include [a6], [a3].
The Wold decomposition of a (weakly) stationary stochastic process $\{ x _ { t } : t \in \mathbf{Z} \}$, $x _ { t } : \Omega \rightarrow \mathbf{R} ^ { n }$, provides interesting insights in the structure of such processes and, in particular, is an important tool for forecasting (from an infinite past).
The main result can be summarized as:
1) Every (weakly) stationary process $\{ x _ { t } : t \in \mathbf{Z} \}$ can uniquely be decomposed as
\begin{equation*} x _ { t } = y _ { t } + z _ { t }, \end{equation*}
where the stationary processes $( y _ { t } )$ and $( z _ { t } )$ are obtained by causal linear transformations of $( x _ { t } )$ (where "causal" means that, e.g. $y _ { t }$, only depends on $x _ { s }$, $s \leq t$), $( y _ { t } )$ and $( z _ { t } )$ are mutually uncorrelated, $( y _ { t } )$ is linearly regular (i.e. the best linear least squares predictors converge to zero, if the forecasting horizon tends to infinity) and $( z _ { t } )$ is linearly singular (i.e. the prediction errors for the best linear least squares predictors are zero).
2) Every linearly regular process $( y _ { t } )$ can be represented as
\begin{equation} \tag{a1} y _ { t } = \sum _ { j = 0 } ^ { \infty } K _ { j } \varepsilon _ { t - j }, \end{equation}
\begin{equation*} K _ { j } \in {\bf R} ^ { n \times n } , K _ { 0 } = I , \sum _ { j = 0 } ^ { \infty } \| K _ { j } \| ^ { 2 } < \infty , \end{equation*}
where $\varepsilon _ { t }$ is white noise (i.e. $\mathsf{E} \varepsilon _ { t } = 0$, $\mathsf{E} \varepsilon _ { t } \varepsilon _ { s } ^ { \prime } = \delta _ { s t } \Sigma$) and $\varepsilon _ { t }$ is obtained by a causal linear transformation of $( y _ { t } )$.
The construction behind the Wold decomposition in the Hilbert space $H$ spanned by the one-dimensional process variables $x _ { t } ^ { ( i ) }$ is as follows: If $H _ { x } ( t )$ denotes the subspace spanned by $\left\{ x _ { s } ^ { ( i ) } : s \leq t ,\, i = 1 , \dots , n \right\}$, then $z _ { t } ^ { ( i ) }$ is obtained from projecting $x _ { t } ^ { ( i ) }$ on the space 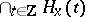 , and $\varepsilon _ { t } ^ { (i) }$ is obtained as the perpendicular by projecting $y _ { t } ^ { ( i ) }$ on the space $H _ { y } ( t - 1 )$ spanned by $\left\{ y _ { s } ^ { ( i ) } : s < t ,\; i = 1 , \dots , n \right\}$. Thus $\varepsilon _ { t }$ is the innovation and the one-step-ahead prediction error for $y _ { t }$ as well as for $x _ { t }$.
, and $\varepsilon _ { t } ^ { (i) }$ is obtained as the perpendicular by projecting $y _ { t } ^ { ( i ) }$ on the space $H _ { y } ( t - 1 )$ spanned by $\left\{ y _ { s } ^ { ( i ) } : s < t ,\; i = 1 , \dots , n \right\}$. Thus $\varepsilon _ { t }$ is the innovation and the one-step-ahead prediction error for $y _ { t }$ as well as for $x _ { t }$.
The implications of the above-mentioned results for (linear least squares) prediction are straightforward: Since $( y _ { t } )$ and $( z _ { t } )$ are orthogonal and since $H _ { x } ( t )$ is the direct sum of $H _ { y } ( t )$ and $H _ { z } ( t )$, the prediction problem can be solved for the linearly regular and the linearly singular part separately, and for a linearly regular process $( y _ { t } )$, $H _ { y } ( t ) = H _ { \epsilon } ( t )$ implies that the best linear least squares $r$-step ahead predictor for $y _ { t+r} $ is given by
\begin{equation*} \hat { y } _ { t , r } = \sum _ { j = r } ^ { \infty } K _ { j } \varepsilon _ { t + r - j } \end{equation*}
and thus the prediction error is
\begin{equation*} y _ { t + r } - \hat { y } _ { t , r } = \sum _ { j = 0 } ^ { r - 1 } K _ { j } \varepsilon _ { t + r - j }. \end{equation*}
Thus, when the representation (a1) is available, the prediction problem for a linearly regular process can be solved.
The next problem is to obtain (a1) from the second moments of $( y _ { t } )$ (cf. also Moment). The problem of determining the coefficients $K_j$ of the Wold representation (a1) (or, equivalently, of determining the corresponding transfer function $k ( e ^ { - i \lambda } ) = \sum _ { j = 0 } ^ { \infty } K _ { j } e ^ { - i \lambda j }$) from the spectral density
\begin{equation} \tag{a2} f ( \lambda ) = ( 2 \pi ) ^ { - 1 } k ( e ^ { - i \lambda } ) \Sigma k ^ { * } ( e ^ { - i \lambda } ), \end{equation}
(where the $*$ denotes the conjugate transpose) of a linearly regular process $( y _ { t } )$, is called the spectral factorization problem. The following result holds:
3) A stationary process $( y _ { t } )$ with a spectral density $f$, which is non-singular $\lambda$-a.e., is linearly regular if and only if
\begin{equation*} \int _ { - \pi } ^ { \pi } \operatorname { log } \operatorname { det } f ( \lambda ) d \lambda > - \infty. \end{equation*}
In this case the factorization $( k , \Sigma )$ in (a2) corresponding to the Wold representation (a1) satisfies the relation
\begin{equation*} \operatorname { det } \Sigma = \operatorname { exp } \left\{ ( 2 \pi ) ^ { - 1 } \int _ { - \pi } ^ { \pi } \operatorname { log } \operatorname { det } 2 \pi f ( \lambda ) d \lambda \right\}. \end{equation*}
The most important special case is that of rational spectral densities; for such one has (see e.g. [a4]):
4) Any rational and $\lambda$-a.e. non-singular spectral density $f$ can be uniquely factorized, such that $k ( z )$ (the extension of $k ( e ^ { - i \lambda } )$ to $\mathbf{C}$) is rational, analytic within a circle containing the closed unit disc, $\operatorname { det } k ( z ) \neq 0$, $| z | < 1$, $k ( 0 ) = I$ (and thus corresponds to the Wold representation (a1)), and $\Sigma > 0$. Then (a1) is the solution of a stable and miniphase ARMA or a (linear) finite-dimensional state space system.
Evidently, the Wold representation (a1) relates stationary processes to linear systems with white noise inputs. Actually, Wold introduced (a1) as a joint representation for AR and MA systems (cf. also Mixed autoregressive moving-average process).
The Wold representation is used, e.g., for the construction of the state space of a linearly regular process and the construction of state space representations, see [a1], [a4]. As mentioned already, the case of rational transfer functions corresponding to stable and miniphase ARMA or (finite-dimensional) state space systems is by far the most important one. In this case there is a wide class of identification procedures available, which also give estimates of the coefficients $K_j$ from finite data $y _ { 1 } , \dots , y _ { T }$ (see e.g. [a4]).
Another case is that of stationary long memory processes (see e.g. [a2]). In this case, in (a1), $\| \sum _ { j = 0 } ^ { \infty } K _ { j } \| ^ { 2 } = \infty$, so that $f$ is infinity at frequency zero, which causes the long memory effect. Models of this kind, in particular so-called ARFIMA models, have attracted considerable attention in modern econometrics.
References
| [a1] | H. Akaike, "Stochastic theory of minimal realizations" IEEE Trans. Autom. Control , AC-19 (1974) pp. 667–674 |
| [a2] | C.W.J. Granger, R. Joyeux, "An introduction to long memory time series models and fractional differencing" J. Time Ser. Anal. , 1 (1980) pp. 15–39 |
| [a3] | E.J. Hannan, "Multiple time series" , Wiley (1970) |
| [a4] | E.J. Hannan, M. Deistler, "The statistical theory of linear systems" , Wiley (1988) |
| [a5] | A.N. Kolmogorov, "Stationary sequences in Hilbert space" Bull. Moscow State Univ. , 2 : 6 (1941) pp. 1–40 |
| [a6] | Y.A. Rozanov, "Stationary random processes" , Holden Day (1967) |
| [a7] | H. Wold, "Study in the analysis of stationary time series" , Almqvist and Wiksell (1954) (Edition: Second) |
| [a8] | V.N. Zasukhin, "On the theory of multidimensional stationary processes" Dokl. Akad. Nauk SSSR , 33 (1941) pp. 435–437 |
Wold decomposition. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Wold_decomposition&oldid=17678