Wiener integral
An abstract integral of Lebesgue type over sets in an infinite-dimensional function space of functionals defined on these sets. Introduced by N. Wiener in the nineteentwenties in connection with problems on Brownian motion [1], [2].
Let 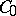 be the vector space of continuous real-valued functions
be the vector space of continuous real-valued functions  defined on
defined on 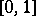 such that
such that 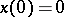 , with norm
, with norm
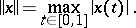 |
The set
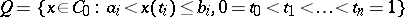 |
is called a quasi-interval of this space. Here, 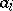 and
and 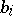 may be equal to
may be equal to 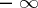 and
and 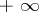 , respectively, but then the symbol
, respectively, but then the symbol 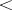 must replace
must replace 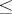 . The whole space
. The whole space 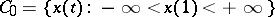 is an example of a quasi-interval.
is an example of a quasi-interval.
The Wiener measure of a quasi-interval 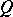 is the number
is the number
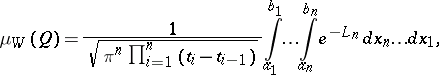 |
where
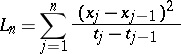 |
and 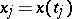 . This measure extends to a
. This measure extends to a 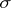 -additive measure on the Borel field of sets generated by the quasi-intervals, known also as Wiener measure.
-additive measure on the Borel field of sets generated by the quasi-intervals, known also as Wiener measure.
Let 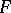 be a functional defined on
be a functional defined on 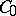 that is measurable with respect to the measure
that is measurable with respect to the measure 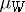 . The Lebesgue-type integral
. The Lebesgue-type integral
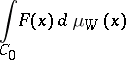 |
is known as the Wiener integral, or as the integral with respect to the Wiener measure, of the functional 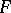 . If
. If 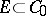 is measurable, then
is measurable, then
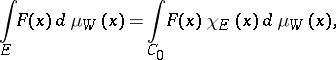 |
where 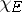 is the characteristic function of the set
is the characteristic function of the set 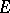 .
.
Wiener's integral displays several properties of the ordinary Lebesgue integral. In particular, a functional which is bounded and measurable on a set 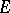 is integrable with respect to the Wiener measure on this set and if, in addition, the functional
is integrable with respect to the Wiener measure on this set and if, in addition, the functional 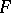 is continuous and non-negative, then
is continuous and non-negative, then
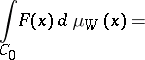 |
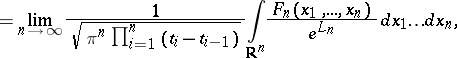 |
where 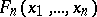 is the value of
is the value of 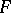 at linear interpolation of
at linear interpolation of 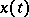 between points
between points 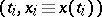 .
.
The computation of a Wiener integral presents considerable difficulties, even for the simplest functionals. The task may sometimes be reduced to solving a single differential equation [1].
There is a method by which Wiener's integral may be approximately computed through approximating it by finite-dimensional Stieltjes integrals of a high multiplicity (cf. Stieltjes integral).
References
| [1] | I.M. Koval'chik, "The Wiener integral" Russian Math. Surveys , 18 : 1 (1963) pp. 97–134 Uspekhi Mat. Nauk , 18 : 1 (1963) pp. 97–134 |
| [2] | G.E. Shilov, "Integration in infinite dimensional spaces and the Wiener integral" Russ. Math. Surveys , 18 : 2 (1963) pp. 99–120 Uspekhi Mat. Nauk , 2 (1963) pp. 99–120 |
Comments
Further references on the computation of Wiener integrals in the sense described above are [a1] and [a2]. In the Western literature, the term "Wiener integral" normally refers to the stochastic integral of a deterministic function 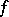 such that
such that 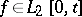 for each
for each 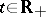 , with respect to the Wiener process
, with respect to the Wiener process 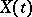 defined on a probability space
defined on a probability space 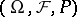 . This is denoted by
. This is denoted by
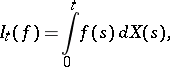 |
and is defined as follows. If 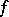 is a simple function, i.e.
is a simple function, i.e. 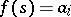 for
for 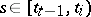 , where
, where 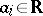 and
and 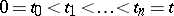 , then
, then
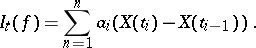 |
Let 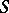 denote the set of simple functions. For
denote the set of simple functions. For 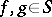 , a computation shows that
, a computation shows that 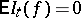 ,
, 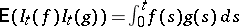 , i.e.
, i.e. 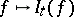 is an inner-product preserving mapping from
is an inner-product preserving mapping from 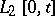 to
to 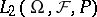 . For any
. For any 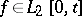 there exists a sequence
there exists a sequence 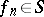 such that
such that 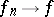 .
. 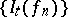 is then a Cauchy sequence in
is then a Cauchy sequence in 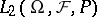 , and one defines
, and one defines
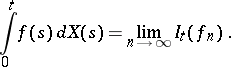 |
Notable features of this construction are as follows.
It is possible to define 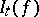 simultaneously for all
simultaneously for all 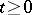 and to obtain a version which is a Gaussian martingale with continuous sample paths
and to obtain a version which is a Gaussian martingale with continuous sample paths
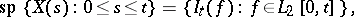 |
where "sp" denotes the closed linear span in 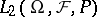 . Information on the Wiener integral in this sense is given in [a3], [a4].
. Information on the Wiener integral in this sense is given in [a3], [a4].
References
| [a1] | A.J. Chorin, "Accurate evaluation of Wiener integrals" Math. Comp. , 27 (1973) pp. 1–15 |
| [a2] | G.L. Blankenschip, J.S. Baras, "Accurate evaluation of stochastic Wiener integrals with applications to scattering in random media and to nonlinear filtering" SIAM J. Appl. Math. , 41 (1981) pp. 518–552 |
| [a3] | M.H.A. Davis, "Linear estimation and stochastic control" , Chapman & Hall (1977) |
| [a4] | R.S. Liptser, A.N. Shiryaev, "Statistics of random processes" , I , Springer (1977) (Translated from Russian) |
| [a5] | J. Yeh, "Stochastic processes and the Wiener integral" , M. Dekker (1973) |
| [a6] | B. Simon, "Functional integration and quantum physics" , Acad. Press (1979) pp. 4–6 |
| [a7] | L.C.G. Rogers, D. Williams, "Diffusions, Markov processes, and martingales" , 2. Itô calculus , Wiley (1987) |
| [a8] | H. Bauer, "Probability theory and elements of measure theory" , Holt, Rinehart & Winston (1972) pp. Chapt. 11 (Translated from German) |
Wiener integral. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Wiener_integral&oldid=17004