Difference between revisions of "Unramified ideal"
(Importing text file) |
m (link) |
||
| Line 7: | Line 7: | ||
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095790/u0957907.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095790/u0957907.png" /></td> </tr></table> | ||
| − | and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095790/u0957908.png" />. More accurately, such an ideal is called absolutely unramified. In general, let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095790/u0957909.png" /> be a [[Dedekind ring|Dedekind ring]] with field of fractions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095790/u09579010.png" />, let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095790/u09579011.png" /> be a finite extension of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095790/u09579012.png" /> and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095790/u09579013.png" /> be the integral closure of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095790/u09579014.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095790/u09579015.png" /> (cf. [[Integral extension of a ring|Integral extension of a ring]]). A prime ideal <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095790/u09579016.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095790/u09579017.png" /> lying over an ideal <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095790/u09579018.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095790/u09579019.png" /> is unramified in the extension <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095790/u09579020.png" /> if | + | and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095790/u0957908.png" />. More accurately, such an ideal is called absolutely unramified. In general, let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095790/u0957909.png" /> be a [[Dedekind ring|Dedekind ring]] with [[field of fractions]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095790/u09579010.png" />, let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095790/u09579011.png" /> be a finite extension of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095790/u09579012.png" /> and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095790/u09579013.png" /> be the integral closure of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095790/u09579014.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095790/u09579015.png" /> (cf. [[Integral extension of a ring|Integral extension of a ring]]). A prime ideal <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095790/u09579016.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095790/u09579017.png" /> lying over an ideal <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095790/u09579018.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095790/u09579019.png" /> is unramified in the extension <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095790/u09579020.png" /> if |
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095790/u09579021.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095790/u09579021.png" /></td> </tr></table> | ||
Revision as of 21:20, 28 November 2014
A prime ideal 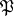 of an algebraic number field
of an algebraic number field 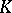 (cf. also Algebraic number; Number field) lying over a prime number
(cf. also Algebraic number; Number field) lying over a prime number 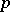 such that the principal ideal
such that the principal ideal 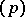 has in
has in  a product decomposition into prime ideals of the form
a product decomposition into prime ideals of the form
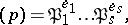 |
where
 |
and  . More accurately, such an ideal is called absolutely unramified. In general, let
. More accurately, such an ideal is called absolutely unramified. In general, let 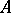 be a Dedekind ring with field of fractions
be a Dedekind ring with field of fractions 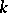 , let
, let 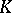 be a finite extension of
be a finite extension of  and let
and let 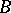 be the integral closure of
be the integral closure of 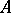 in
in 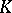 (cf. Integral extension of a ring). A prime ideal
(cf. Integral extension of a ring). A prime ideal 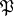 of
of 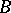 lying over an ideal
lying over an ideal 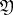 of
of  is unramified in the extension
is unramified in the extension 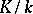 if
if
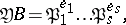 |
where 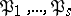 are pairwise distinct prime ideals of
are pairwise distinct prime ideals of 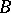 ,
, 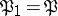 and
and  . If all ideals
. If all ideals 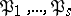 are unramified, then one occasionally says that
are unramified, then one occasionally says that 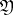 remains unramified in
remains unramified in 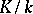 . For a Galois extension
. For a Galois extension 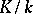 , an ideal
, an ideal 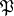 of
of 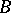 is unramified if and only if the decomposition group of
is unramified if and only if the decomposition group of 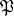 in the Galois group
in the Galois group 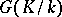 is the same as the Galois group of the extension of the residue class field
is the same as the Galois group of the extension of the residue class field 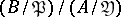 . In any finite extension of algebraic number fields all ideals except finitely many are unramified.
. In any finite extension of algebraic number fields all ideals except finitely many are unramified.
References
| [1] | Z.I. Borevich, I.R. Shafarevich, "Number theory" , Acad. Press (1966) (Translated from Russian) (German translation: Birkhäuser, 1966) |
| [2] | S. Lang, "Algebraic number theory" , Addison-Wesley (1970) |
| [3] | J.W.S. Cassels (ed.) A. Fröhlich (ed.) , Algebraic number theory , Acad. Press (1986) |
Unramified ideal. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Unramified_ideal&oldid=14372