Universal function

for a given (countable) class 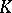of functions of type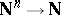

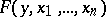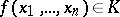A function of type such that for any function there exists an 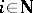for which

(*)

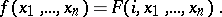Here, 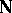is the set of natural numbers and the equation (*) means that the functions 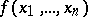and 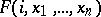are defined for the same set of arguments, and their values on this set coincide. Sometimes it is required in the definition of a universal function that for each the function lies in 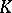(cf. [4]). There are a number of other variants of the definition of a universal function (cf. [1], [2]).

A universal function exists for every countable class of functions. The following universal functions play an important role in the theory of algorithms: 1) universal partial recursive functions for the class of all -place 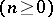partial recursive functions (cf. Partial recursive function); and 2) universal general recursive functions for the class of all -place primitive recursive functions (cf. Primitive recursive function).

If a function 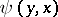is universal for the class of all one-place partial recursive functions, then it cannot be extended to a total recursive function, and the set 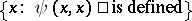is an example of a recursively-enumerable, but not recursive, set of natural numbers (cf. also Enumerable set).

References

[1]	R. Peter, "Recursive functions" , Acad. Press (1967) (Translated from German)
[2]	S.C. Kleene, "Introduction to metamathematics" , North-Holland (1951)
[3]	V.A. Uspenskii, "Leçons sur les fonctions calculables" , Hermann (1966) (Translated from Russian)
[4]	A.I. Mal'tsev, "Algorithms and recursive functions" , Wolters-Noordhoff (1970) (Translated from Russian)

References

[a1]	H. Rogers jr., "Theory of recursive functions and effective computability" , McGraw-Hill (1967) pp. 164–165