Teichmüller mapping
Let 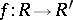 be a quasi-conformal mapping from a Riemann surface
be a quasi-conformal mapping from a Riemann surface  onto a Riemann surface
onto a Riemann surface 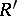 . Let
. Let 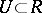 be a neighbourhood with local parameter
be a neighbourhood with local parameter  ,
, 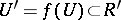 . The complex dilatation of
. The complex dilatation of 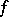 in terms of
in terms of  is
is 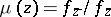 , with
, with 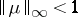 ; invariantly written, it reads
; invariantly written, it reads 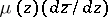 . The quasi-conformal mapping mapping
. The quasi-conformal mapping mapping 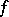 is called a Teichmüller mapping if its complex dilatation is of the form
is called a Teichmüller mapping if its complex dilatation is of the form
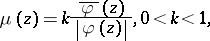 |
where 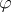 is an analytic quadratic differential on
is an analytic quadratic differential on 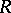 , possibly with isolated singularities. (The surface is usually punctured at these points.) The norm of
, possibly with isolated singularities. (The surface is usually punctured at these points.) The norm of 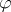 is defined to be
is defined to be 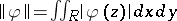 ,
, 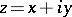 ; if it is finite, the singularities can be first-order poles at worst. If
; if it is finite, the singularities can be first-order poles at worst. If 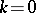 , the mapping
, the mapping 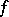 is conformal (cf. also Conformal mapping) and there is no specific quadratic differential associated with it.
is conformal (cf. also Conformal mapping) and there is no specific quadratic differential associated with it.
One introduces, locally and outside the set 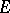 of critical points (zeros and isolated singularities of
of critical points (zeros and isolated singularities of 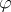 ), the function
), the function
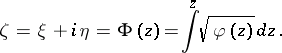 |
Since 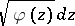 is a first-order differential, the local function elements of
is a first-order differential, the local function elements of 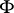 are well determined up to the transformation
are well determined up to the transformation 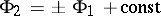 . In any sufficiently small neighbourhood
. In any sufficiently small neighbourhood  which does not contain a critical point, the function
which does not contain a critical point, the function  is a univalent conformal mapping from
is a univalent conformal mapping from 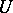 onto a neighbourhood
onto a neighbourhood 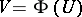 in the
in the 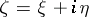 -plane (cf. also Univalent function). Map
-plane (cf. also Univalent function). Map 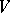 by the horizontal stretching
by the horizontal stretching  ,
, 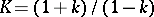 , onto a neighbourhood
, onto a neighbourhood 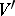 . It is easy to see that
. It is easy to see that 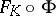 has the same complex dilatation as
has the same complex dilatation as 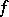 . Therefore,
. Therefore, 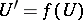 and
and 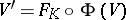 are related by a conformal mapping
are related by a conformal mapping 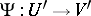 , with
, with  . The square of its derivative
. The square of its derivative 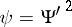 is a holomorphic quadratic differential on
is a holomorphic quadratic differential on 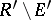 ,
, 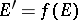 . The points in
. The points in 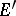 are the critical points of
are the critical points of 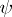 , and corresponding points have the same order, positive for zeros, negative for poles. Thus, to every Teichmüller mapping
, and corresponding points have the same order, positive for zeros, negative for poles. Thus, to every Teichmüller mapping 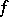 there is associated a pair of quadratic differentials,
there is associated a pair of quadratic differentials, 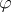 on
on 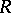 and
and 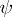 on
on 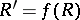 . The horizontal trajectories of
. The horizontal trajectories of 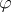 go over into Euclidean horizontal straight lines in the
go over into Euclidean horizontal straight lines in the 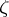 -plane. It is immediate that they are stretched by
-plane. It is immediate that they are stretched by 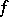 onto the horizontal trajectories of
onto the horizontal trajectories of 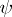 , whereas the vertical trajectories of
, whereas the vertical trajectories of 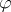 are just shifted into those of
are just shifted into those of 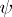 .
.
An important subclass of the class of Teichmüller mappings is the one associated with quadratic differentials of finite norm 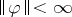 (the same is then true for
(the same is then true for 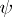 , since
, since 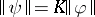 ). These mappings are uniquely extremal for their boundary values [a3]. Of course, they have the property that their dilatation
). These mappings are uniquely extremal for their boundary values [a3]. Of course, they have the property that their dilatation 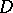 is constant (
is constant (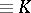 ). Quite recently (1998) it has been shown that there are uniquely extremal quasi-conformal mappings with non-constant dilatation [a2]. Thus, there are quasi-symmetric boundary homeomorphisms of the unit disc for which there is no extremal extension into the disc which is of Teichmüller form, contrary to an idea of O. Teichmüller in [a1], pp. 184–185.
). Quite recently (1998) it has been shown that there are uniquely extremal quasi-conformal mappings with non-constant dilatation [a2]. Thus, there are quasi-symmetric boundary homeomorphisms of the unit disc for which there is no extremal extension into the disc which is of Teichmüller form, contrary to an idea of O. Teichmüller in [a1], pp. 184–185.
References
| [a1] | O. Teichmüller, "Extremale quasikonforme Abbildungen und quadratische Differentiale" Abh. Preuss. Akad. Wiss., Math.-naturw. Kl. 22 , 197 (1939) |
| [a2] | V. Božin, N. Lakic, V. Markovič, M. Mateljevič, "Unique extremality" J. d'Anal. Math. , to appear (1999) |
| [a3] | E. Reich, K. Strebel, "Extremal quasiconformal mappings with given boundary values" , Contributions to Analysis , Acad. Press (1974) pp. 375–392 |
Teichmüller mapping. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Teichm%C3%BCller_mapping&oldid=17397