Sorgenfrey topology
right half-open interval topology
A topology  on the real line
on the real line 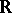 (cf. also Topological structure (topology)) defined by declaring that a set
(cf. also Topological structure (topology)) defined by declaring that a set 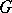 is open in
is open in  if for any
if for any 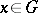 there is an
there is an 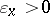 such that
such that 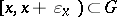 .
. 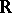 endowed with the topology
endowed with the topology  is termed the Sorgenfrey line, and is denoted by
is termed the Sorgenfrey line, and is denoted by 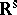 .
.
The Sorgenfrey line serves as a counterexample to several topological properties, see, for example, [a3]. For example, it is not metrizable (cf. also Metrizable space) but it is Hausdorff and perfectly normal (cf. also Hausdorff space; Perfectly-normal space). It is first countable but not second countable (cf. also First axiom of countability; Second axiom of countability). Moreover, the Sorgenfrey line is hereditarily Lindelöf, zero dimensional and paracompact (cf. also Lindelöf space; Zero-dimensional space; Paracompact space). Any compact subset of the Sorgenfrey line is countable and nowhere dense in the usual Euclidean topology (cf. Nowhere-dense set). The Sorgenfrey topology is neither locally compact nor locally connected (cf. also Locally compact space; Locally connected space).
Consider the Cartesian product 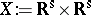 equipped with the product topology (cf. also Topological product), which is called the Sorgenfrey half-open square topology. Then
equipped with the product topology (cf. also Topological product), which is called the Sorgenfrey half-open square topology. Then 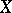 is completely regular but not normal (cf. Completely-regular space; Normal space). It is separable (cf. Separable space) but neither Lindelöf nor countably paracompact.
is completely regular but not normal (cf. Completely-regular space; Normal space). It is separable (cf. Separable space) but neither Lindelöf nor countably paracompact.
Many further properties of the Sorgenfrey topology are examined in detail in [a1]. Namely, the Sorgenfrey topology is a fine topology on the real line, and 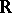 equipped with both the Sorgenfrey topology and the Euclidean topology serves as an example of a bitopological space (that is, a space endowed with two topological structures). The Sorgenfrey topology satisfies the condition (tFL) when studying fine limits (if a real-valued function
equipped with both the Sorgenfrey topology and the Euclidean topology serves as an example of a bitopological space (that is, a space endowed with two topological structures). The Sorgenfrey topology satisfies the condition (tFL) when studying fine limits (if a real-valued function 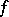 has a limit at the point
has a limit at the point  with respect to the Sorgenfrey topology
with respect to the Sorgenfrey topology  it has the same limit at
it has the same limit at  with respect to the Euclidean topology when restricted to a
with respect to the Euclidean topology when restricted to a  -neighbourhood of
-neighbourhood of  ). It has also the
). It has also the 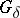 -insertion property (given a subset
-insertion property (given a subset 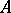 of
of 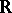 , there is a
, there is a 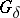 -subset
-subset  of
of  such that
such that  lies in between the
lies in between the  -interior and the
-interior and the  -closure of
-closure of 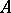 ). The Sorgenfrey topology satisfies the so-called essential radius condition: For any point
). The Sorgenfrey topology satisfies the so-called essential radius condition: For any point  and any
and any  -neighbourhood
-neighbourhood 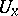 of
of  there is an "essential radius"
there is an "essential radius" 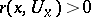 such that whenever the distance of two points
such that whenever the distance of two points  and
and 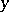 is majorized by
is majorized by 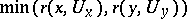 , then
, then 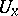 and
and 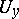 intersect. The real line
intersect. The real line 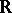 equipped with the Sorgenfrey topology and the Euclidean topology is a binormal bitopological space, while
equipped with the Sorgenfrey topology and the Euclidean topology is a binormal bitopological space, while 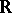 with the Sorgenfrey and the density topology is not binormal. See [a1] for answers to interesting questions concerning the class of continuous functions in the Sorgenfrey topology and for functions of the first or second Baire classes.
with the Sorgenfrey and the density topology is not binormal. See [a1] for answers to interesting questions concerning the class of continuous functions in the Sorgenfrey topology and for functions of the first or second Baire classes.
References
| [a1] | J. Lukeš, J. Malý, L. Zajíček, "Fine topology methods in real analysis and potential theory" , Lecture Notes in Mathematics , 1189 , Springer (1986) |
| [a2] | R.H. Sorgenfrey, "On the topological product of paracompact spaces" Bull. Amer. Math. Soc. , 53 (1947) pp. 631–632 |
| [a3] | A.S. Steen, J.A. Seebach Jr., "Counterexamples in topology" , Springer (1978) |
Sorgenfrey topology. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Sorgenfrey_topology&oldid=13306