Sokhotskii formulas
Formulas first discovered by Yu.V. Sokhotskii [1], expressing the boundary values of a Cauchy-type integral. With more complete proofs but significantly later, the formulas were obtained independently by J. Plemelj .
Let $ \Gamma $: $ t= t( s) $, $ 0\leq s \leq l $, $ t( 0)= t( l) $, be a closed smooth Jordan curve in the complex $ z $- plane, let $ \phi ( t) $ be the complex density in a Cauchy-type integral along $ \Gamma $, on which $ \phi ( t) $ satisfies a Hölder condition:
$$ | \phi ( t _ {1} ) - \phi ( t _ {2} ) | \leq C | t _ {1} - t _ {2} | ^ \alpha ,\ 0< \alpha \leq 1; $$
let $ D ^ {+} $ be the interior of $ \Gamma $, $ D ^ {-} $ its exterior, and let
$$ \tag{1 } \Phi ( z) = \frac{1}{2 \pi i } \int\limits _ \Gamma \frac{\phi ( t) dt }{t-} z ,\ z \notin \Gamma , $$
be a Cauchy-type integral. Then, for any point $ t _ {0} \in \Gamma $ the limits
$$ \Phi ^ {+} ( t _ {0} ) = \lim\limits _ {\begin{array}{c} z \rightarrow t _ {0} \\ z \in D ^ {+} \end{array} } \Phi ( z), $$
$$ \Phi ^ {-} ( t _ {0} ) = \lim\limits _ {\begin{array}{c} z \rightarrow t _ {0} \\ z \in D ^ {-} \end{array} } \Phi ( z) $$
exist and are given by the Sokhotskii formulas
$$ \tag{2 } \left . or, equivalently, $$ \Phi ^ {+} ( t _ {0} ) + \Phi ^ {-} ( t _ {0} ) = \frac{1}{\pi i }
\int\limits _ \Gamma
\frac{\phi ( t) dt }{t- t _ {0} }
,
$$ $$ \Phi ^ {+} ( t _ {0} ) - \Phi ^ {-} ( t _ {0} ) = \phi ( t _ {0} ) . $$ The integrals along $ \Gamma $ on the right-hand sides of these formulas are understood in the sense of the Cauchy principal value and are so-called singular integrals. By taking, under these conditions, $ \Phi ^ {+} ( t) $( or $ \Phi ^ {-} ( t) $) as values of the integral $ \Phi ( z) $ on $ \Gamma $, one thus obtains a function $ \Phi ( z) $ that is continuous in the closed domain $ \overline{ {D ^ {+} }}\; = D ^ {+} \cup \Gamma $( respectively, $ \overline{ {D ^ {-} }}\; = D ^ {-} \cup \Gamma $). In the large, $ \Phi ( z) $ is sometimes described as a piecewise-analytic function. If $ \alpha < 1 $, then $ \Phi ^ {+} ( t) $ and $ \Phi ^ {-} ( t) $ are also Hölder continuous on $ \Gamma $ with the same exponent $ \alpha $, while if $ \alpha = 1 $, with any exponent $ \alpha ^ \prime < 1 $. For the corner points $ t _ {0} $ of a piecewise-smooth curve $ \Gamma $( see Fig.), the Sokhotskii formulas take the form $$ \tag{3 }
In the case of a non-closed piecewise-smooth curve $ \Gamma $, the Sokhotskii formulas (2) and (3) remain valid for the interior points of the arc $ \Gamma $.
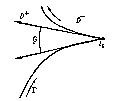
Figure: s086020a
The Sokhotskii formulas play a basic role in solving boundary value problems of function theory and in the theory of singular integral equations (see [3], [5]), and also in solving various applied problems in function theory (see [4]).
The question naturally arises as to the possibility of extending the conditions on the contour $ \Gamma $ and the density $ \phi ( t) $, in such a way that the Sokhotskii formulas (possibly with some restrictions) remain valid. The most significant results in this direction are due to V.V. Golubev and I.I. Privalov (see [6], [8]). For example, let $ \Gamma $ be a rectifiable Jordan curve, and let the density $ \phi ( t) $ be, as before, Hölder continuous on $ \Gamma $. Then the Sokhotskii formulas (2) hold almost everywhere on $ \Gamma $, where $ \Phi ^ {+} ( t _ {0} ) $ and $ \Phi ^ {-} ( t _ {0} ) $ are understood as non-tangential boundary values of the Cauchy-type integral from inside and outside $ \Gamma $, respectively, but $ \Phi ^ {+} ( z) $ and $ \Phi ^ {-} ( z) $ are, in general, not continuous in the closed domains $ \overline{ {D ^ {+} }}\; $ and $ \overline{ {D ^ {-} }}\; $.
For spatial analogues of the Sokhotskii formulas see [7].
References
| [1] | Yu.V. Sokhotskii, "On definite integrals and functions used in series expansions" , St. Petersburg (1873) (In Russian) (Dissertation) |
| [2a] | J. Plemelj, "Ein Ergänzungssatz zur Cauchyschen Integraldarstellung analytischer Funktionen, Randwerte betreffend" Monatsh. Math. Phys. , 19 (1908) pp. 205–210 |
| [2b] | J. Plemelj, "Riemannsche Funktionenscharen mit gegebener Monodromiegruppe" Monatsh. Math. Phys. , 19 (1908) pp. 211–245 |
| [3] | N.I. Muskhelishvili, "Singular integral equations" , Wolters-Noordhoff (1972) (Translated from Russian) |
| [4] | N.I. Muskhelishvili, "Some basic problems of the mathematical theory of elasticity" , Noordhoff (1975) (Translated from Russian) |
| [5] | F.D. Gakhov, "Boundary value problems" , Pergamon (1966) (Translated from Russian) |
| [6] | I.I. [I.I. Privalov] Priwalow, "Randeigenschaften analytischer Funktionen" , Deutsch. Verlag Wissenschaft. (1956) (Translated from Russian) |
| [7] | A.V. Bitsadze, "Fundamentals of the theory of analytic functions of a complex variable" , Moscow (1972) (In Russian) |
| [8] | B.V. Khvedelidze, "The method of Cauchy-type integrals in the discontinuous boundary value problems of the theory of holomorphic functions of a complex variable" J. Soviet Math. , 7 (1977) pp. 309–415 Itogi Nauk. Sovremen. Probl. Mat. , 7 (1975) pp. 5–162 |
Comments
In the Western literature one usually speaks of the Plemelj formulas; the combination Sokhotskii–Plemelj formulas also occurs.
Much work has been done on Cauchy-type integrals in recent years. Thus, A.P. Calderón [a1] has proved the existence of non-tangential boundary values almost everywhere under weaker conditions, and he has studied the principal value integral, or Cauchy transform, in (2) as a bounded linear operator on appropriate $ L _ {p} $ spaces. For further information see [a2].
The idea of representing a function on a simple closed curve as the jump of an analytic function across that curve has been extensively generalized. Thus, every distribution on the unit circle and every tempered distribution on $ \mathbf R $ can be represented as such jumps in an appropriate sense, cf. [a3]. The ultimate in this direction are Sato's hyperfunctions (cf. [a5] and Hyperfunction).
References
| [a1] | A.P. Calderón, "Cauchy integrals on Lipschitz curves and related operators" Proc. Nat. Acad. Sci. USA , 74 : 4 (1977) pp. 1324–1327 |
| [a2] | V.P. Khavin (ed.) S.V. Khrushchev (ed.) N.K. Nikol'skii (ed.) , Linear and complex analysis problem book , Lect. notes in math. , 1043 , Springer (1984) pp. Chapt. 6 (Translated from Russian) |
| [a3] | H.G. Tillmann, "Darstellung der Schwartzschen Distributionen durch analytischer Funktionen" Math. Z. , 77 (1961) pp. 106–124 |
| [a4] | M. Sato, "Theory of hyperfunctions I-II" J. Fac. Sci. Univ. Tokyo I , 8 (1959–1960) pp. 139–193; 387–437 |
| [a5] | L.V. Hörmander, "The analysis of linear partial differential operators" , 1 , Springer (1983) |
Sokhotskii formulas. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Sokhotskii_formulas&oldid=12269