Difference between revisions of "Separate and joint continuity"
(Importing text file) |
m (links) |
||
| Line 1: | Line 1: | ||
| − | It follows from a property of the product topology that every [[ | + | It follows from a property of the [[product topology]] that every [[continuous function]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120100/s1201001.png" /> between [[topological space]]s is separately continuous, i.e., <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120100/s1201002.png" /> is continuous with respect to each variable while the other variable is fixed [[#References|[a3]]]. It was observed by E. Heine [[#References|[a14]]], p. 15, that, in general, the converse does not hold (see also [[#References|[a11]]] for an account of early discoveries in this field). |
| − | Given "nice" topological spaces <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120100/s1201003.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120100/s1201004.png" /> | + | Given "nice" topological spaces <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120100/s1201003.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120100/s1201004.png" />, let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120100/s1201005.png" /> be a [[metric space]] and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120100/s1201006.png" /> be separately continuous. Questions on separate and joint continuity are, among others, problems of the type: |
the existence problem: Find the set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120100/s1201007.png" /> of points of continuity of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120100/s1201008.png" />. | the existence problem: Find the set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120100/s1201007.png" /> of points of continuity of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120100/s1201008.png" />. | ||
| − | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120100/s1201009.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120100/s12010010.png" /> are "nice" , then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120100/s12010011.png" /> is a dense <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120100/s12010012.png" />-subset (cf. [[Set of type F sigma(G delta)|Set of type | + | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120100/s1201009.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120100/s12010010.png" /> are "nice" , then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120100/s12010011.png" /> is a dense <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120100/s12010012.png" />-subset (cf. [[Set of type F sigma(G delta)|Set of type $F_\sigma$ ($G_\delta$)]]) of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120100/s12010015.png" />. For example, every real-valued separately continuous function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120100/s12010016.png" /> is of the first Baire class (cf. also [[Baire classes]]), hence <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120100/s12010017.png" /> is a dense <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120100/s12010018.png" />-subset. |
There is also interest in a "fibre" version; it is the same as above, except now one looks for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120100/s12010019.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120100/s12010020.png" />, for any fixed <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120100/s12010021.png" />. | There is also interest in a "fibre" version; it is the same as above, except now one looks for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120100/s12010019.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120100/s12010020.png" />, for any fixed <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120100/s12010021.png" />. | ||
| Line 15: | Line 15: | ||
The uniformization problem. Find out whether there is a dense <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120100/s12010027.png" />-subset <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120100/s12010028.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120100/s12010029.png" /> such that the set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120100/s12010030.png" /> is contained in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120100/s12010031.png" />. | The uniformization problem. Find out whether there is a dense <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120100/s12010027.png" />-subset <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120100/s12010028.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120100/s12010029.png" /> such that the set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120100/s12010030.png" /> is contained in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120100/s12010031.png" />. | ||
| − | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120100/s12010032.png" />, such a result was known already to R. Baire [[#References|[a1]]]. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120100/s12010033.png" /> is a complete metric space, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120100/s12010034.png" /> is a compact metric space and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120100/s12010035.png" />, the uniformization problem was positively solved by H. Hahn [[#References|[a7]]]. I. Namioka [[#References|[a9]]] extended Hahn's result to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120100/s12010036.png" /> being a regular, strongly countably complete space, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120100/s12010037.png" /> being a locally compact <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120100/s12010038.png" />-compact space and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120100/s12010039.png" /> being a pseudo-metric space. | + | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120100/s12010032.png" />, such a result was known already to R. Baire [[#References|[a1]]]. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120100/s12010033.png" /> is a complete metric space, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120100/s12010034.png" /> is a compact metric space and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120100/s12010035.png" />, the uniformization problem was positively solved by H. Hahn [[#References|[a7]]]. I. Namioka [[#References|[a9]]] extended Hahn's result to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120100/s12010036.png" /> being a regular, [[strongly countably complete topological space]], <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120100/s12010037.png" /> being a locally compact <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120100/s12010038.png" />-compact space and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120100/s12010039.png" /> being a pseudo-metric space. |
| − | Following [[#References|[a4]]], one says that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120100/s12010040.png" /> is a Namioka space if for any compact space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120100/s12010041.png" />, any metric space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120100/s12010042.png" /> and any separately continuous function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120100/s12010043.png" />, the uniformization problem can be positively solved. M. Talagrand [[#References|[a13]]] constructed an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120100/s12010045.png" />-favourable space (hence, a Baire space) that is not Namioka. J. Saint Ramond [[#References|[a12]]] proved that separable Baire | + | Following [[#References|[a4]]], one says that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120100/s12010040.png" /> is a ''[[Namioka space]]'' if for any compact space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120100/s12010041.png" />, any metric space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120100/s12010042.png" /> and any separately continuous function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120100/s12010043.png" />, the uniformization problem can be positively solved. M. Talagrand [[#References|[a13]]] constructed an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120100/s12010045.png" />-favourable space (hence, a Baire space) that is not Namioka. J. Saint Ramond [[#References|[a12]]] proved that [[Separable space|separable]] [[Baire space]]s are Namioka, Namioka [[Tikhonov space]]s are Baire, while in the class of metric spaces, the set of Namioka spaces and the set of Baire spaces coincide. |
A space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120100/s12010046.png" /> is a co-Namioka space if for any Baire space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120100/s12010047.png" />, any metric space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120100/s12010048.png" /> and for any separably continuous function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120100/s12010049.png" />, the uniformization problem can be positively solved. For example, Corson-compact spaces are co–Namioka, whereas the Čech–Stone compactification <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120100/s12010050.png" /> is not. Many results in this direction have been obtained by R. Haydon, R.W. Hansell, J.E. Jain, J.P. Troallic, Namioka, and R. Pol (see [[#References|[a10]]] for a comprehensive exposition of this topic, organizing research in this field until the middle of the 1980s). | A space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120100/s12010046.png" /> is a co-Namioka space if for any Baire space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120100/s12010047.png" />, any metric space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120100/s12010048.png" /> and for any separably continuous function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120100/s12010049.png" />, the uniformization problem can be positively solved. For example, Corson-compact spaces are co–Namioka, whereas the Čech–Stone compactification <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120100/s12010050.png" /> is not. Many results in this direction have been obtained by R. Haydon, R.W. Hansell, J.E. Jain, J.P. Troallic, Namioka, and R. Pol (see [[#References|[a10]]] for a comprehensive exposition of this topic, organizing research in this field until the middle of the 1980s). | ||
==Applications.== | ==Applications.== | ||
| − | R. Ellis [[#References|[a5]]], [[#References|[a6]]] showed that every locally compact semi-topological group (i.e., a group endowed with a topology for which the product is separately continuous) is a [[ | + | R. Ellis [[#References|[a5]]], [[#References|[a6]]] showed that every locally compact semi-topological group (i.e., a group endowed with a topology for which the product is separately continuous) is a [[topological group]]. Using methods of separate and joint continuity, A. Bouziad [[#References|[a2]]] extended Ellis' theorem to all Čech-analytic Baire semi-topological groups (hence, to all Čech-complete semi-topological groups). |
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> R. Baire, "Sur les fonctions des variables réelles" ''Ann. Mat. Pura Appl.'' , '''3''' (1899) pp. 1–122</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> A. Bouziad, "Every Čech-analytic Baire semitopological group is a topological group" ''Proc. Amer. Math. Soc.'' , '''124''' (1996) pp. 953–959</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> A.L. Cauchy, "Cours d'Analyse de l'Ecole Polytechnique" (1821)</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> J.P.R. Christensen, "Joint continuity of separately continuous functions" ''Proc. Amer. Math. Soc.'' , '''82''' (1981) pp. 455–462</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> R. Ellis, "A note on the continuity of the inverse" ''Proc. Amer. Math. Soc.'' , '''8''' (1957) pp. 372–373</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> R. Ellis, "Locally compact transformation groups" ''Duke Math. J.'' , '''24''' (1957) pp. 119–125</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> H. Hahn, "Reelle Funktionen" , Akad. Verlag (1932) pp. 325–338</TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> R. Kershner, "The continuity of functions of many variables" ''Trans. Amer. Math. Soc.'' , '''53''' (1943) pp. 83–100</TD></TR><TR><TD valign="top">[a9]</TD> <TD valign="top"> I. Namioka, "Separate and joint continuity" ''Pacific J. Math.'' , '''51''' (1974) pp. 515–531</TD></TR><TR><TD valign="top">[a10]</TD> <TD valign="top"> Z. Piotrowski, "Separate and joint continuity" ''Real Anal. Exch.'' , '''11''' (1985-86) pp. 293–322</TD></TR><TR><TD valign="top">[a11]</TD> <TD valign="top"> Z. Piotrowski, "The genesis of separate versus joint continuity" ''Tatra Mtn. Math. Publ.'' , '''8''' (1996) pp. 113–126</TD></TR><TR><TD valign="top">[a12]</TD> <TD valign="top"> J. Saint Raymond, "Jeux topologiques et espaces de Namioka" ''Proc. Amer. Math. Soc.'' , '''87''' (1983) pp. 499–504</TD></TR><TR><TD valign="top">[a13]</TD> <TD valign="top"> M. Talagrand, "Espaces de Baire et espaces de Namioka" ''Math. Ann.'' , '''270''' (1985) pp. 159–164</TD></TR><TR><TD valign="top">[a14]</TD> <TD valign="top"> J. Thomae, "Abriss einer Theorie der complexen Funktionen" , Louis Nebert Verlag (1873) (Edition: Second)</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> R. Baire, "Sur les fonctions des variables réelles" ''Ann. Mat. Pura Appl.'' , '''3''' (1899) pp. 1–122</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> A. Bouziad, "Every Čech-analytic Baire semitopological group is a topological group" ''Proc. Amer. Math. Soc.'' , '''124''' (1996) pp. 953–959</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> A.L. Cauchy, "Cours d'Analyse de l'Ecole Polytechnique" (1821)</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> J.P.R. Christensen, "Joint continuity of separately continuous functions" ''Proc. Amer. Math. Soc.'' , '''82''' (1981) pp. 455–462</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> R. Ellis, "A note on the continuity of the inverse" ''Proc. Amer. Math. Soc.'' , '''8''' (1957) pp. 372–373</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> R. Ellis, "Locally compact transformation groups" ''Duke Math. J.'' , '''24''' (1957) pp. 119–125</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> H. Hahn, "Reelle Funktionen" , Akad. Verlag (1932) pp. 325–338</TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> R. Kershner, "The continuity of functions of many variables" ''Trans. Amer. Math. Soc.'' , '''53''' (1943) pp. 83–100</TD></TR><TR><TD valign="top">[a9]</TD> <TD valign="top"> I. Namioka, "Separate and joint continuity" ''Pacific J. Math.'' , '''51''' (1974) pp. 515–531</TD></TR><TR><TD valign="top">[a10]</TD> <TD valign="top"> Z. Piotrowski, "Separate and joint continuity" ''Real Anal. Exch.'' , '''11''' (1985-86) pp. 293–322</TD></TR><TR><TD valign="top">[a11]</TD> <TD valign="top"> Z. Piotrowski, "The genesis of separate versus joint continuity" ''Tatra Mtn. Math. Publ.'' , '''8''' (1996) pp. 113–126</TD></TR><TR><TD valign="top">[a12]</TD> <TD valign="top"> J. Saint Raymond, "Jeux topologiques et espaces de Namioka" ''Proc. Amer. Math. Soc.'' , '''87''' (1983) pp. 499–504</TD></TR><TR><TD valign="top">[a13]</TD> <TD valign="top"> M. Talagrand, "Espaces de Baire et espaces de Namioka" ''Math. Ann.'' , '''270''' (1985) pp. 159–164</TD></TR><TR><TD valign="top">[a14]</TD> <TD valign="top"> J. Thomae, "Abriss einer Theorie der complexen Funktionen" , Louis Nebert Verlag (1873) (Edition: Second)</TD></TR></table> | ||
Revision as of 22:02, 2 January 2016
It follows from a property of the product topology that every continuous function 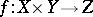 between topological spaces is separately continuous, i.e.,
between topological spaces is separately continuous, i.e., 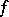 is continuous with respect to each variable while the other variable is fixed [a3]. It was observed by E. Heine [a14], p. 15, that, in general, the converse does not hold (see also [a11] for an account of early discoveries in this field).
is continuous with respect to each variable while the other variable is fixed [a3]. It was observed by E. Heine [a14], p. 15, that, in general, the converse does not hold (see also [a11] for an account of early discoveries in this field).
Given "nice" topological spaces 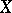 and
and 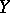 , let
, let 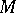 be a metric space and let
be a metric space and let 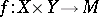 be separately continuous. Questions on separate and joint continuity are, among others, problems of the type:
be separately continuous. Questions on separate and joint continuity are, among others, problems of the type:
the existence problem: Find the set 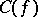 of points of continuity of
of points of continuity of 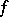 .
.
If 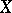 and
and 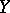 are "nice" , then
are "nice" , then 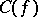 is a dense
is a dense 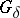 -subset (cf. Set of type $F_\sigma$ ($G_\delta$)) of
-subset (cf. Set of type $F_\sigma$ ($G_\delta$)) of 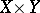 . For example, every real-valued separately continuous function
. For example, every real-valued separately continuous function 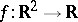 is of the first Baire class (cf. also Baire classes), hence
is of the first Baire class (cf. also Baire classes), hence 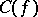 is a dense
is a dense 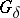 -subset.
-subset.
There is also interest in a "fibre" version; it is the same as above, except now one looks for 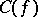 in
in 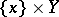 , for any fixed
, for any fixed 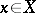 .
.
The characterization problem. Characterize 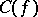 as a subset of
as a subset of 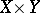 .
.
If 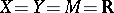 , then the set
, then the set 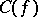 is the complement of an
is the complement of an 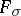 -set contained in the product of two sets of the first Baire category [a8].
-set contained in the product of two sets of the first Baire category [a8].
The uniformization problem. Find out whether there is a dense 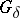 -subset
-subset 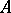 of
of 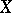 such that the set
such that the set 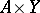 is contained in
is contained in 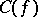 .
.
If 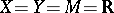 , such a result was known already to R. Baire [a1]. If
, such a result was known already to R. Baire [a1]. If 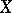 is a complete metric space,
is a complete metric space, 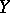 is a compact metric space and
is a compact metric space and 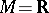 , the uniformization problem was positively solved by H. Hahn [a7]. I. Namioka [a9] extended Hahn's result to
, the uniformization problem was positively solved by H. Hahn [a7]. I. Namioka [a9] extended Hahn's result to 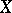 being a regular, strongly countably complete topological space,
being a regular, strongly countably complete topological space, 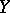 being a locally compact
being a locally compact 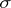 -compact space and
-compact space and 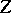 being a pseudo-metric space.
being a pseudo-metric space.
Following [a4], one says that 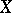 is a Namioka space if for any compact space
is a Namioka space if for any compact space 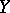 , any metric space
, any metric space 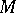 and any separately continuous function
and any separately continuous function 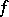 , the uniformization problem can be positively solved. M. Talagrand [a13] constructed an
, the uniformization problem can be positively solved. M. Talagrand [a13] constructed an  -favourable space (hence, a Baire space) that is not Namioka. J. Saint Ramond [a12] proved that separable Baire spaces are Namioka, Namioka Tikhonov spaces are Baire, while in the class of metric spaces, the set of Namioka spaces and the set of Baire spaces coincide.
-favourable space (hence, a Baire space) that is not Namioka. J. Saint Ramond [a12] proved that separable Baire spaces are Namioka, Namioka Tikhonov spaces are Baire, while in the class of metric spaces, the set of Namioka spaces and the set of Baire spaces coincide.
A space 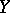 is a co-Namioka space if for any Baire space
is a co-Namioka space if for any Baire space 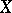 , any metric space
, any metric space 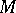 and for any separably continuous function
and for any separably continuous function 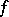 , the uniformization problem can be positively solved. For example, Corson-compact spaces are co–Namioka, whereas the Čech–Stone compactification
, the uniformization problem can be positively solved. For example, Corson-compact spaces are co–Namioka, whereas the Čech–Stone compactification 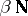 is not. Many results in this direction have been obtained by R. Haydon, R.W. Hansell, J.E. Jain, J.P. Troallic, Namioka, and R. Pol (see [a10] for a comprehensive exposition of this topic, organizing research in this field until the middle of the 1980s).
is not. Many results in this direction have been obtained by R. Haydon, R.W. Hansell, J.E. Jain, J.P. Troallic, Namioka, and R. Pol (see [a10] for a comprehensive exposition of this topic, organizing research in this field until the middle of the 1980s).
Applications.
R. Ellis [a5], [a6] showed that every locally compact semi-topological group (i.e., a group endowed with a topology for which the product is separately continuous) is a topological group. Using methods of separate and joint continuity, A. Bouziad [a2] extended Ellis' theorem to all Čech-analytic Baire semi-topological groups (hence, to all Čech-complete semi-topological groups).
References
| [a1] | R. Baire, "Sur les fonctions des variables réelles" Ann. Mat. Pura Appl. , 3 (1899) pp. 1–122 |
| [a2] | A. Bouziad, "Every Čech-analytic Baire semitopological group is a topological group" Proc. Amer. Math. Soc. , 124 (1996) pp. 953–959 |
| [a3] | A.L. Cauchy, "Cours d'Analyse de l'Ecole Polytechnique" (1821) |
| [a4] | J.P.R. Christensen, "Joint continuity of separately continuous functions" Proc. Amer. Math. Soc. , 82 (1981) pp. 455–462 |
| [a5] | R. Ellis, "A note on the continuity of the inverse" Proc. Amer. Math. Soc. , 8 (1957) pp. 372–373 |
| [a6] | R. Ellis, "Locally compact transformation groups" Duke Math. J. , 24 (1957) pp. 119–125 |
| [a7] | H. Hahn, "Reelle Funktionen" , Akad. Verlag (1932) pp. 325–338 |
| [a8] | R. Kershner, "The continuity of functions of many variables" Trans. Amer. Math. Soc. , 53 (1943) pp. 83–100 |
| [a9] | I. Namioka, "Separate and joint continuity" Pacific J. Math. , 51 (1974) pp. 515–531 |
| [a10] | Z. Piotrowski, "Separate and joint continuity" Real Anal. Exch. , 11 (1985-86) pp. 293–322 |
| [a11] | Z. Piotrowski, "The genesis of separate versus joint continuity" Tatra Mtn. Math. Publ. , 8 (1996) pp. 113–126 |
| [a12] | J. Saint Raymond, "Jeux topologiques et espaces de Namioka" Proc. Amer. Math. Soc. , 87 (1983) pp. 499–504 |
| [a13] | M. Talagrand, "Espaces de Baire et espaces de Namioka" Math. Ann. , 270 (1985) pp. 159–164 |
| [a14] | J. Thomae, "Abriss einer Theorie der complexen Funktionen" , Louis Nebert Verlag (1873) (Edition: Second) |
Separate and joint continuity. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Separate_and_joint_continuity&oldid=12039