Difference between revisions of "Semi-simple element"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 8: | Line 8: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> A. Borel, "Linear algebraic groups" , Benjamin (1969) {{MR|0251042}} {{ZBL|0206.49801}} {{ZBL|0186.33201}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> Yu.I. Merzlyakov, "Rational groups" , Moscow (1980) (In Russian) {{MR|0602700}} {{ZBL|0518.20032}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> J.E. Humphreys, "Linear algebraic groups" , Springer (1975) {{MR|0396773}} {{ZBL|0325.20039}} </TD></TR></table> |
| Line 18: | Line 18: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> J.E. Humphreys, "Introduction to Lie algebras and representation theory" , Springer (1972) pp. §5.4 {{MR|0323842}} {{ZBL|0254.17004}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> J.-P. Serre, "Lie algebras and Lie groups" , Benjamin (1965) pp. LA6.14 (Translated from French) {{MR|0218496}} {{ZBL|0132.27803}} </TD></TR></table> |
Revision as of 14:51, 24 March 2012
of a linear algebraic group 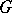
An element 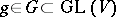 , where
, where 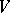 is a finite-dimensional vector space over an algebraically closed field
is a finite-dimensional vector space over an algebraically closed field 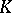 , which is a semi-simple endomorphism of the space
, which is a semi-simple endomorphism of the space 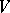 , i.e. is diagonalizable. The notion of a semi-simple element of
, i.e. is diagonalizable. The notion of a semi-simple element of 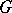 is intrinsic, i.e. is determined by the algebraic group structure of
is intrinsic, i.e. is determined by the algebraic group structure of 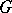 only and does not depend on the choice of a faithful representation
only and does not depend on the choice of a faithful representation 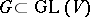 as a closed algebraic subgroup of a general linear group. An element
as a closed algebraic subgroup of a general linear group. An element 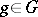 is semi-simple if and only if the right translation operator
is semi-simple if and only if the right translation operator 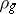 in
in 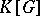 is diagonalizable. For any rational linear representation
is diagonalizable. For any rational linear representation 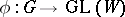 , the set of semi-simple elements of the group
, the set of semi-simple elements of the group  is mapped onto the set of semi-simple elements of the group
is mapped onto the set of semi-simple elements of the group 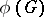 .
.
Analogously one defines semi-simple elements of the algebraic Lie algebra 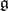 of
of 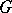 ; the differential
; the differential 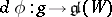 of the representation
of the representation 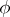 maps the set of semi-simple elements of the algebra
maps the set of semi-simple elements of the algebra 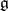 onto the set of semi-simple elements of its image.
onto the set of semi-simple elements of its image.
By definition, a semi-simple element of an abstract Lie algebra 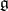 is an element
is an element 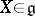 for which the adjoint linear transformation
for which the adjoint linear transformation  is a semi-simple endomorphism of the vector space
is a semi-simple endomorphism of the vector space 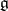 . If
. If 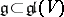 is the Lie algebra of a reductive linear algebraic group, then
is the Lie algebra of a reductive linear algebraic group, then  is a semi-simple element of the algebra
is a semi-simple element of the algebra 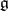 if and only if
if and only if 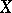 is a semi-simple endomorphism of
is a semi-simple endomorphism of 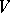 .
.
References
| [1] | A. Borel, "Linear algebraic groups" , Benjamin (1969) MR0251042 Zbl 0206.49801 Zbl 0186.33201 |
| [2] | Yu.I. Merzlyakov, "Rational groups" , Moscow (1980) (In Russian) MR0602700 Zbl 0518.20032 |
| [3] | J.E. Humphreys, "Linear algebraic groups" , Springer (1975) MR0396773 Zbl 0325.20039 |
Comments
Thus, the notions of a semi-simple element for an algebraic Lie algebra (the Lie algebra of a linear algebraic group) and for an abstract Lie algebra do not necessarily coincide. But they do so for the Lie algebras of reductive linear algebraic groups (and semi-simple Lie algebras). To avoid this confusion, an element 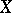 of an abstract Lie algebra
of an abstract Lie algebra 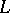 such that ad
such that ad 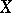 is a semi-simple endomorphism of
is a semi-simple endomorphism of 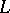 is sometimes called
is sometimes called 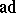 -semi-simple.
-semi-simple.
Cf. also Jordan decomposition, 2).
References
| [a1] | J.E. Humphreys, "Introduction to Lie algebras and representation theory" , Springer (1972) pp. §5.4 MR0323842 Zbl 0254.17004 |
| [a2] | J.-P. Serre, "Lie algebras and Lie groups" , Benjamin (1965) pp. LA6.14 (Translated from French) MR0218496 Zbl 0132.27803 |
Semi-simple element. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Semi-simple_element&oldid=18504