Schur multiplicator
Schur multiplier, of a group 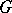
The cohomology group 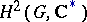 , where
, where 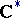 is the multiplicative group of complex numbers with trivial
is the multiplicative group of complex numbers with trivial 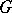 -action. The Schur multiplicator was introduced by I. Schur [1] in his work on finite-dimensional complex projective representations of a group (cf. Projective representation). If
-action. The Schur multiplicator was introduced by I. Schur [1] in his work on finite-dimensional complex projective representations of a group (cf. Projective representation). If 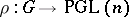 is such a representation, then
is such a representation, then 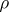 can be interpreted as a mapping
can be interpreted as a mapping 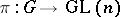 such that
such that
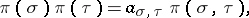 |
where 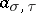 is a
is a  -cocycle with values in
-cocycle with values in 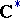 . In particular, the projective representation
. In particular, the projective representation 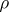 is the projectivization of a linear representation
is the projectivization of a linear representation 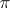 if and only if the cocycle
if and only if the cocycle 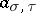 determines the trivial element of the group
determines the trivial element of the group 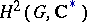 . If
. If 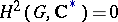 , then
, then 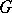 is called a closed group in the sense of Schur. If
is called a closed group in the sense of Schur. If 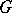 is a finite group, then there exist natural isomorphisms
is a finite group, then there exist natural isomorphisms
 |
Let 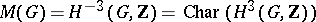 . If a central extension
. If a central extension
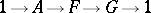 | (*) |
of a finite group 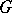 is given, then there is a natural mapping
is given, then there is a natural mapping 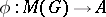 whose image coincides with
whose image coincides with 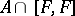 . This mapping
. This mapping 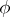 coincides with the mapping
coincides with the mapping 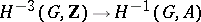 induced by the cup-product with the element of
induced by the cup-product with the element of 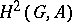 defined by the extension (*). Conversely, for any subgroup
defined by the extension (*). Conversely, for any subgroup 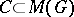 there is an extension (*) such that
there is an extension (*) such that 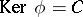 . If
. If 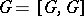 , then the extension (*) is uniquely determined by the homomorphism
, then the extension (*) is uniquely determined by the homomorphism 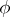 . If
. If 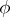 is a monomorphism, then any projective representation of
is a monomorphism, then any projective representation of 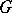 is induced by some linear representation of
is induced by some linear representation of 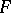 .
.
References
| [1] | I. Schur, "Ueber die Darstellung der endlichen Gruppen durch gebrochene lineare Substitutionen" J. Reine Angew. Math. , 127 (1904) pp. 20–50 |
| [2] | S. MacLane, "Homology" , Springer (1975) |
Comments
References
| [a1] | G. Gruenberg, "Cohomological topics in group theory" , Lect. notes in math. , 143 , Springer (1970) |
| [a2] | C.W. Curtis, I. Reiner, "Methods of representation theory" , I , Wiley (Interscience) (1981) |
Schur multiplicator. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Schur_multiplicator&oldid=12190