Saddle surface
A generalization of a surface of negative curvature (cf. Negative curvature, surface of). Let  be a surface in the
be a surface in the  -dimensional Euclidean space
-dimensional Euclidean space  defined by an immersion
defined by an immersion  of a two-dimensional manifold
of a two-dimensional manifold  in
in  . A plane
. A plane  cuts off a crust from
cuts off a crust from  if among the components of the inverse image of the set
if among the components of the inverse image of the set  in
in  there is one with a compact closure. The part of
there is one with a compact closure. The part of 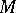 that corresponds to this component is called a crust (see Fig.).
that corresponds to this component is called a crust (see Fig.).

Figure: s083080a
The surface 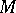 is called a saddle surface if it is impossible to cut off a crust by any plane. Examples of saddle surfaces are a one-sheet hyperboloid, a hyperbolic paraboloid and a ruled surface. For a twice continuously-differentiable surface to be a saddle surface it is necessary and sufficient that at each point of the surface its Gaussian curvature is non-positive. A surface for which all its points are saddle points (cf. Saddle point) is a saddle surface.
is called a saddle surface if it is impossible to cut off a crust by any plane. Examples of saddle surfaces are a one-sheet hyperboloid, a hyperbolic paraboloid and a ruled surface. For a twice continuously-differentiable surface to be a saddle surface it is necessary and sufficient that at each point of the surface its Gaussian curvature is non-positive. A surface for which all its points are saddle points (cf. Saddle point) is a saddle surface.
A saddle surface that is bounded by a rectifiable contour is, with respect to its intrinsic metric induced by the metric of the space, a two-dimensional manifold of non-positive curvature. A number of properties of surfaces of negative curvature can be generalized to the class of saddle surfaces, but it seems that these surfaces do not form such a natural class of surfaces as do convex surfaces.
References
| [1] | I.Ya. Bakel'man, A.L. Verner, B.E. Kantor, "Introduction to differential geometry "in the large" " , Moscow (1973) (In Russian) |
| [2] | S.Z. Shefel', "Studies on the geometry of saddle-like surfaces" , Novosibirsk (1963) (In Russian) |
Comments
References
| [a1] | J.C.C. Nitsche, "Vorlesungen über Minimalflächen" , Springer (1975) pp. §455 |
Saddle surface. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Saddle_surface&oldid=17506