Riedtmann classification
A finite-dimensional algebra 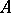 over an algebraically closed field
over an algebraically closed field 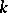 is called self-injective if
is called self-injective if 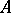 , considered as a right
, considered as a right 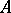 -module, is injective (cf. also Injective module). Well-known examples for self-injective algebras are the group algebras
-module, is injective (cf. also Injective module). Well-known examples for self-injective algebras are the group algebras 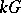 for finite groups
for finite groups 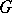 (cf. also Group algebra). An arbitrary finite-dimensional algebra
(cf. also Group algebra). An arbitrary finite-dimensional algebra 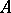 is said to be representation-finite provided that there are only finitely many isomorphism classes of indecomposable finite-dimensional right
is said to be representation-finite provided that there are only finitely many isomorphism classes of indecomposable finite-dimensional right 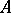 -modules.
-modules.
C. Riedtmann made the main contribution to the classification of all self-injective algebras that are representation-finite. Her key idea was not to look at the algebra 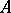 itself, but rather at its Auslander–Reiten quiver
itself, but rather at its Auslander–Reiten quiver 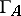 . (Quiver is an abbreviation for directed graph, see Quiver.) The vertices of the Auslander–Reiten quiver (see also Representation of an associative algebra) are the isomorphism classes of finite-dimensional
. (Quiver is an abbreviation for directed graph, see Quiver.) The vertices of the Auslander–Reiten quiver (see also Representation of an associative algebra) are the isomorphism classes of finite-dimensional 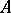 -modules. The number of arrows from the isomorphism class of
-modules. The number of arrows from the isomorphism class of 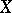 to the isomorphism class of
to the isomorphism class of 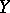 is the dimension of the space
is the dimension of the space 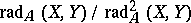 , where
, where 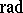 is the Jacobson radical of the category of all finite-dimensional
is the Jacobson radical of the category of all finite-dimensional 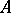 -modules. The Auslander–Reiten quiver is a translation quiver, which means that it carries an additional structure, namely a translation
-modules. The Auslander–Reiten quiver is a translation quiver, which means that it carries an additional structure, namely a translation 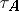 mapping the non-projective vertices bijectively to the non-injective vertices. The translation is induced by the existence of almost-spit sequences
mapping the non-projective vertices bijectively to the non-injective vertices. The translation is induced by the existence of almost-spit sequences 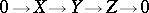 (see also Representation of an associative algebra; Almost-split sequence) and sends the isomorphism class of a non-projective indecomposable module
(see also Representation of an associative algebra; Almost-split sequence) and sends the isomorphism class of a non-projective indecomposable module 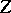 to the starting term
to the starting term 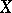 .
.
The stable part  of the Auslander–Reiten quiver
of the Auslander–Reiten quiver 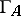 of
of 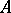 is the full subquiver of
is the full subquiver of  given by the modules that cannot be shifted into an injective or projective vertex by a power
given by the modules that cannot be shifted into an injective or projective vertex by a power 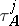 for some integer
for some integer 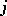 . In [a3], Riedtmann succeeded to prove that for any connected representation-finite finite-dimensional
. In [a3], Riedtmann succeeded to prove that for any connected representation-finite finite-dimensional 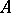 the stable part
the stable part 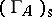 of the Auslander–Reiten quiver is of the shape
of the Auslander–Reiten quiver is of the shape 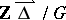 , where
, where 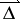 is a quiver whose underlying graph
is a quiver whose underlying graph 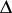 is a Dynkin diagram
is a Dynkin diagram 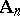 (
(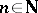 ),
),  (
(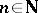 ,
,  ), or
), or 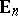 (
( ) and
) and 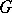 is an infinite cyclic group of automorphisms of the translation quiver
is an infinite cyclic group of automorphisms of the translation quiver 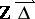 . The vertices of
. The vertices of 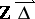 are the pairs
are the pairs  such that
such that 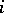 is an integer and
is an integer and  a vertex of
a vertex of 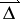 . From
. From 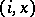 to
to 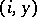 there are the arrows
there are the arrows 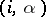 with
with 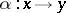 an arrow of
an arrow of 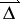 . In addition, from
. In addition, from 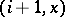 to
to 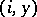 there exist the arrows
there exist the arrows 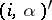 with
with  an arrow of
an arrow of 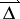 . The translation maps
. The translation maps 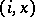 to
to 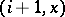 .
.
For a self-injective algebra 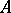 , the only vertices of the Auslander–Reiten quiver that do not belong to
, the only vertices of the Auslander–Reiten quiver that do not belong to 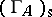 are the isomorphism classes of the indecomposable projective (and injective) modules. Thus, one can reconstruct
are the isomorphism classes of the indecomposable projective (and injective) modules. Thus, one can reconstruct 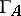 from
from 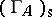 by finding in
by finding in 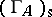 the starting points of arrows of
the starting points of arrows of 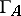 ending in projective vertices. These combinatorial data are called a configuration. This shows that for finding all possible Auslander–Reiten quivers
ending in projective vertices. These combinatorial data are called a configuration. This shows that for finding all possible Auslander–Reiten quivers 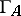 of all connected representation-finite self-injective algebras
of all connected representation-finite self-injective algebras  one has to classify the infinite cyclic automorphism groups
one has to classify the infinite cyclic automorphism groups  of
of 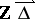 and the
and the 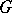 -invariant configurations of
-invariant configurations of 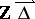 for all Dynkin diagrams. For the Dynkin diagrams
for all Dynkin diagrams. For the Dynkin diagrams 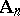 and
and 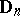 this classification was carried out in [a4] and [a5].
this classification was carried out in [a4] and [a5].
The classification of the possible configurations for the exceptional Dynkin diagrams 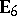 ,
, 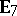 ,
, 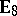 turned out to be more difficult. Fortunately, the development of tilting theory offered a convenient way for a solution. Namely, it was observed in [a1] and [a2] that in order to equip
turned out to be more difficult. Fortunately, the development of tilting theory offered a convenient way for a solution. Namely, it was observed in [a1] and [a2] that in order to equip 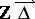 with all possible configurations, one has to form the Auslander–Reiten quivers of the repetitive algebras of the tilted algebras of representation-finite hereditary algebras of type
with all possible configurations, one has to form the Auslander–Reiten quivers of the repetitive algebras of the tilted algebras of representation-finite hereditary algebras of type 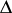 (cf. also Tilted algebra). Nevertheless, the full classification of all these repetitive algebras eventually obtained in [a7] required the use of a computer for handling the huge amount of structures appearing in the case
(cf. also Tilted algebra). Nevertheless, the full classification of all these repetitive algebras eventually obtained in [a7] required the use of a computer for handling the huge amount of structures appearing in the case 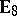 .
.
If one finally wants to return from the Auslander–Reiten quiver 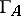 to the algebra
to the algebra 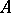 itself, one considers the factor of the free
itself, one considers the factor of the free  -linear category of
-linear category of 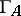 by the mesh relations induced by the almost-split sequences. This factor is called the mesh category of
by the mesh relations induced by the almost-split sequences. This factor is called the mesh category of  . Forming the endomorphism algebra of the direct sum of all projective objects in this mesh category yields
. Forming the endomorphism algebra of the direct sum of all projective objects in this mesh category yields 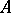 (up to Morita equivalence), provided that
(up to Morita equivalence), provided that 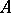 is standard (i.e. the mesh category is equivalent to the category of indecomposable finite-dimensional
is standard (i.e. the mesh category is equivalent to the category of indecomposable finite-dimensional 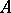 -modules). Non-standard algebras appear only if the characteristic of the field
-modules). Non-standard algebras appear only if the characteristic of the field 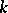 is
is  and
and 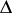 is of type
is of type  . They were classified in [a6] and [a9].
. They were classified in [a6] and [a9].
It is worth noting that the approach using repetitive algebras was generalized in order to classify the representation-tame self-injective standard algebras of polynomial growth in [a8]. In this case tilted algebras of representation-tame hereditary and canonical algebras replace the tilted algebras of representation-finite hereditary algebras.
References
| [a1] | O. Bretscher, C. Läser, C. Riedtmann, "Selfinjective and simply connected algebras" Manuscripta Math. , 36 (1981/82) pp. 253–307 |
| [a2] | D. Hughes, J. Waschbüsch, "Trivial extensions of tilted algebras" Proc. London Math. Soc. , 46 (1983) pp. 347–364 |
| [a3] | C. Riedtmann, "Algebren, Darstellungen, Überlagerungen und zurück" Comment. Math. Helv. , 55 (1980) pp. 199–224 |
| [a4] | C. Riedtmann, "Representation-finite selfinjective algebras of class 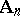 " , Representation theory II , Lecture Notes in Mathematics , 832 , Springer (1981) pp. 449–520 " , Representation theory II , Lecture Notes in Mathematics , 832 , Springer (1981) pp. 449–520 |
| [a5] | C. Riedtmann, "Configurations of 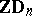 " J. Algebra , 82 (1983) pp. 309–327 " J. Algebra , 82 (1983) pp. 309–327 |
| [a6] | C. Riedtmann, "Representation-finite self-injective algebras of class 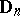 " Compositio Math. , 49 (1983) pp. 231–282 " Compositio Math. , 49 (1983) pp. 231–282 |
| [a7] | B. Roggon, "Selfinjective and iterated tilted algebras of type 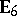 , , 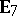 , , 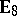 " , E 95-008 SFB , 343 , Bielefeld (1995) " , E 95-008 SFB , 343 , Bielefeld (1995) |
| [a8] | A. Skowroński, "Selfinjective algebras of polynomial growth" Math. Ann. , 285 (1989) pp. 177–199 |
| [a9] | J. Waschbüsch, "Symmetrische Algebren vom endlichen Modultyp" J. Reine Angew. Math. , 321 (1981) pp. 78–98 |
Riedtmann classification. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Riedtmann_classification&oldid=14608