Random allocation
A probability scheme in which  particles are randomly distributed over
particles are randomly distributed over 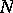 cells. In the simplest scheme, the particles are distributed equi-probably and independently of one another, so that each can fall into any fixed cell with a probability of
cells. In the simplest scheme, the particles are distributed equi-probably and independently of one another, so that each can fall into any fixed cell with a probability of  . Let
. Let 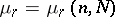 be the number of cells in which, after distribution, there are exactly
be the number of cells in which, after distribution, there are exactly  particles, and let
particles, and let 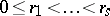 .
.
The generating function
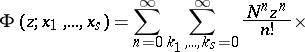 |
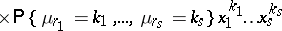 |
has the following form:
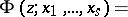 | (1) |
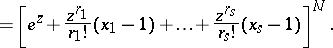 |
The generating function (1) allows one to compute the moments of the 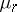 and to study the asymptotic properties of their distribution as
and to study the asymptotic properties of their distribution as 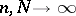 . These asymptotic properties are to a large extent determined by the behaviour of the parameter
. These asymptotic properties are to a large extent determined by the behaviour of the parameter 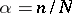 — the average number of particles in a cell. If
— the average number of particles in a cell. If 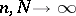 and
and 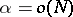 , then for fixed
, then for fixed  and
and 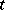 ,
,
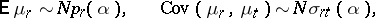 | (2) |
where 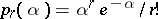 ,
,
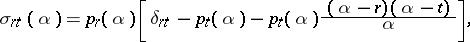 |
and 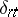 is the Kronecker delta. One can identify five domains with different types of asymptotic behaviour of
is the Kronecker delta. One can identify five domains with different types of asymptotic behaviour of 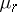 as
as 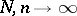 .
.
The central domain corresponds to 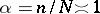 . The domain for which
. The domain for which
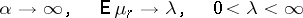 |
is called the right  -domain, and the right intermediate
-domain, and the right intermediate  -domain is that for which
-domain is that for which
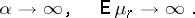 |
For 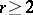 , the left
, the left  -domain corresponds to the case where
-domain corresponds to the case where
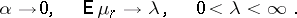 |
The left intermediate  -domain is that for which
-domain is that for which
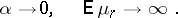 |
The left and right intermediate  -domains for
-domains for 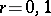 are identified with the corresponding
are identified with the corresponding  -domains.
-domains.
In the case of an equi-probable scheme, 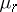 has asymptotically a Poisson distribution in the right
has asymptotically a Poisson distribution in the right  -domains. The same is true in the left
-domains. The same is true in the left  -domains when
-domains when 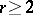 , and when
, and when 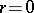 or
or 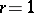 ,
,  and
and 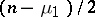 have Poisson distributions in the limit. In the left and right intermediate
have Poisson distributions in the limit. In the left and right intermediate  -domains the
-domains the 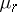 have asymptotically a normal distribution. In the central domain there is a multi-dimensional asymptotic normality theorem for
have asymptotically a normal distribution. In the central domain there is a multi-dimensional asymptotic normality theorem for 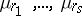 ; the parameters of the limiting normal distribution are defined by the asymptotic formulas (2) (see [1]).
; the parameters of the limiting normal distribution are defined by the asymptotic formulas (2) (see [1]).
An allocation in which  particles are distributed over
particles are distributed over 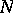 cells independently of each other in such a way that the probability of each of the particles falling into the
cells independently of each other in such a way that the probability of each of the particles falling into the 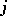 -th cell is equal to
-th cell is equal to 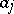 ,
, 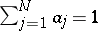 , is called polynomial. For a polynomial allocation one can also introduce central, right and left domains, and limiting normal and Poisson theorems hold (see [1], [3]). Using these theorems, it is possible to calculate the power of the empty-boxes test (cf. also Power of a statistical test). Let
, is called polynomial. For a polynomial allocation one can also introduce central, right and left domains, and limiting normal and Poisson theorems hold (see [1], [3]). Using these theorems, it is possible to calculate the power of the empty-boxes test (cf. also Power of a statistical test). Let 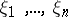 be independent random variables each having a continuous distribution function
be independent random variables each having a continuous distribution function 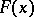 (hypothesis
(hypothesis 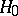 ). The alternative hypothesis
). The alternative hypothesis 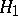 corresponds to another distribution function
corresponds to another distribution function 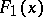 . The points
. The points 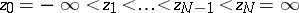 are chosen in such a way that
are chosen in such a way that 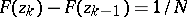 ,
, 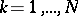 . The empty-boxes test is based on the statistic
. The empty-boxes test is based on the statistic 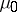 , equal to the number of intervals
, equal to the number of intervals 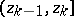 containing none of the
containing none of the 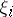 . The empty-boxes test is determined by the critical region
. The empty-boxes test is determined by the critical region 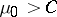 , where
, where 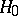 is rejected. Since under
is rejected. Since under 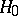 ,
, 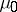 has a probability distribution defined by a uniform allocation, whereas under
has a probability distribution defined by a uniform allocation, whereas under 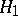 it has a distribution defined by a polynomial allocation, it is possible to use limit theorems for
it has a distribution defined by a polynomial allocation, it is possible to use limit theorems for 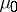 to calculate the power
to calculate the power 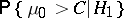 of this test (see [2]).
of this test (see [2]).
In another scheme the particles are grouped in blocks of size 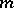 and it is assumed that they are put in the
and it is assumed that they are put in the 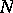 cells in such a way that no two particles from one block fall into the same cell, the positions of the different blocks being independent. If all
cells in such a way that no two particles from one block fall into the same cell, the positions of the different blocks being independent. If all  positions of each block are equi-probable and the number of blocks
positions of each block are equi-probable and the number of blocks 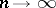 , then for bounded or weakly increasing
, then for bounded or weakly increasing 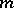 , the
, the 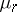 again have asymptotically a normal or Poisson distribution.
again have asymptotically a normal or Poisson distribution.
There are various possible generalizations of allocation schemes (see [1]) connected with a whole series of combinatorial problems of probability theory (random permutations, random mappings, trees, etc.).
References
| [1] | V.F. [V.F. Kolchin] Kolčin, B.A. [B.A. Sevast'yanov] Sevast'janov, V.P. [V.P. Chistyakov] Čistyakov, "Random allocations" , Winston (1978) (Translated from Russian) |
| [2] | B.A. Sevast'yanov, "The empty boxes criterion and its generalizations" Trudy. Inst. Prikl. Mat. Tbilis. Univ. , 2 (1969) pp. 229–233 (In Russian) |
| [3] | V.G. Mikhailov, "The central limit theorem for a scheme for independent allocation of particles in cells" Proc. Steklov Inst. Math. , 157 (1981) pp. 147–164 Trudy Mat. Inst. Steklov. , 157 (1981) pp. 138–152 |
Comments
The problems involved are often referred to as occupancy problems; they are equivalent to urn problems (see [a1] and Urn model).
References
| [a1] | N.L. Johnson, S. Kotz, "Urn models and their application" , Wiley (1977) |
Random allocation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Random_allocation&oldid=14763