Pseudo-group
of transformations of a differentiable manifold 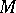
A family of diffeomorphisms from open subsets of 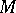 into
into 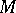 that is closed under composition of mappings, transition to the inverse mapping, as well as under restriction and glueing of mappings. More precisely, a pseudo-group of transformations
that is closed under composition of mappings, transition to the inverse mapping, as well as under restriction and glueing of mappings. More precisely, a pseudo-group of transformations 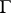 of a manifold
of a manifold 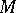 consists of local transformations, i.e. pairs of the form
consists of local transformations, i.e. pairs of the form 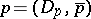 where
where 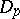 is an open subset of
is an open subset of 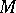 and
and 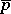 is a diffeomorphism
is a diffeomorphism 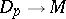 , where it is moreover assumed that 1)
, where it is moreover assumed that 1)  implies
implies 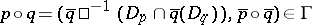 ; 2)
; 2) 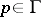 implies
implies 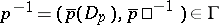 ; 3)
; 3) 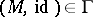 ; and 4) if
; and 4) if 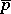 is a diffeomorphism from an open subset
is a diffeomorphism from an open subset 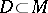 into
into 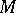 and
and 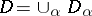 , where
, where  are open sets in
are open sets in 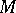 , then
, then 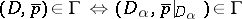 for any
for any 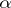 . With necessary changes in 1)–4) one can also define pseudo-groups of transformations of an arbitrary topological space (cf. [7]) or even of an arbitrary set. As a group of transformations, a pseudo-group of transformations determines an equivalence relation on
. With necessary changes in 1)–4) one can also define pseudo-groups of transformations of an arbitrary topological space (cf. [7]) or even of an arbitrary set. As a group of transformations, a pseudo-group of transformations determines an equivalence relation on 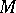 ; the equivalence classes are called its orbits. A pseudo-group
; the equivalence classes are called its orbits. A pseudo-group 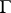 of transformations of a manifold
of transformations of a manifold 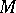 is called transitive if
is called transitive if 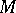 is its only orbit, and is called primitive if
is its only orbit, and is called primitive if 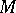 does not admit non-trivial
does not admit non-trivial 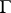 -invariant foliations (otherwise the pseudo-group is called imprimitive).
-invariant foliations (otherwise the pseudo-group is called imprimitive).
A pseudo-group 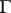 of transformations of a differentiable manifold is called a Lie pseudo-group of transformations defined by a system
of transformations of a differentiable manifold is called a Lie pseudo-group of transformations defined by a system 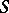 of partial differential equations if
of partial differential equations if 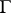 consists of exactly those local transformations of
consists of exactly those local transformations of 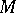 that satisfy the system
that satisfy the system 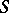 . E.g., the pseudo-group of conformal transformations of the plane is a Lie pseudo-group of transformations, determined by the Cauchy–Riemann equations (cf. Cauchy–Riemann conditions). The order of a Lie pseudo-group of transformations is the minimum order of its defining system of differential equations.
. E.g., the pseudo-group of conformal transformations of the plane is a Lie pseudo-group of transformations, determined by the Cauchy–Riemann equations (cf. Cauchy–Riemann conditions). The order of a Lie pseudo-group of transformations is the minimum order of its defining system of differential equations.
Examples of Lie pseudo-groups of transformations. a) The pseudo-group of all holomorphic local transformations of  -dimensional complex space
-dimensional complex space  .
.
b) The pseudo-group of all holomorphic local transformations of 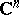 with constant Jacobian.
with constant Jacobian.
c) The pseudo-group of all holomorphic local transformations of 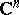 with Jacobian 1.
with Jacobian 1.
d) The Hamilton pseudo-group of all holomorphic local transformations of 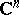 (
( even) preserving the differential
even) preserving the differential  -form
-form
 |
e) The pseudo-group of all holomorphic local transformations of 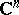 preserving
preserving 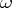 up to constant factor.
up to constant factor.
f) The contact pseudo-group of all holomorphic local transformations of 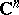 (
(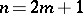 ,
, 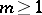 ) preserving the differential
) preserving the differential 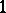 -form
-form
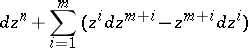 |
up to a factor (which can be a function).
g) The real analogues of the complex pseudo-groups of transformations of Examples a)–f).
The order of the Lie pseudo-groups of Examples a), c)–f) is 1, while in b) the order is 2.
Any Lie group 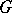 of transformations of a manifold
of transformations of a manifold 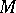 determines a pseudo-group
determines a pseudo-group 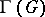 of transformations, consisting of the restrictions of the transformations from
of transformations, consisting of the restrictions of the transformations from 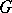 onto open subsets of
onto open subsets of 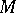 . A pseudo-group of transformations of the form
. A pseudo-group of transformations of the form 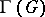 is called globalizable. E.g., a pseudo-group of local conformal transformations of the sphere
is called globalizable. E.g., a pseudo-group of local conformal transformations of the sphere 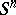 is globalizable for
is globalizable for 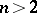 and not globalizable for
and not globalizable for 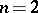 .
.
A Lie pseudo-group of transformations is said to be of finite type if there is a natural number 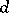 such that every local transformation
such that every local transformation 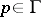 is uniquely determined by its
is uniquely determined by its 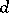 -jet at some point
-jet at some point 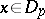 ; the smallest such
; the smallest such 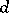 is called the degree, or type, of
is called the degree, or type, of 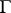 ; if such a
; if such a 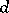 does not exist, then
does not exist, then 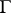 is called a pseudo-group of transformations of infinite type. The pseudo-groups of Examples a)–f) are primitive Lie pseudo-groups of transformations of infinite type.
is called a pseudo-group of transformations of infinite type. The pseudo-groups of Examples a)–f) are primitive Lie pseudo-groups of transformations of infinite type.
Let 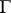 be a transitive Lie pseudo-group of transformations of an
be a transitive Lie pseudo-group of transformations of an  -dimensional manifold
-dimensional manifold 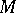 and let
and let  be the family of all
be the family of all  -jets of the local transformations in
-jets of the local transformations in 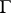 that preserve a point
that preserve a point 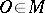 , i.e. those
, i.e. those 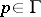 for which
for which 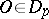 and
and 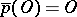 . The set
. The set 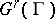 , endowed with the natural structure of a Lie group, is called the
, endowed with the natural structure of a Lie group, is called the  -th order isotropy group of
-th order isotropy group of 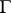 (
(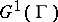 is also called the linear isotropy group of
is also called the linear isotropy group of 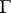 ). The Lie algebra
). The Lie algebra 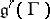 of
of 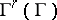 can be naturally imbedded in the Lie algebra of
can be naturally imbedded in the Lie algebra of  -jets of vector fields on
-jets of vector fields on 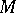 at
at 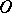 . If
. If 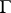 is a Lie pseudo-group of transformations of order one, then the kernel
is a Lie pseudo-group of transformations of order one, then the kernel 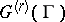 of the natural homomorphism
of the natural homomorphism 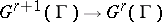 depends, for any
depends, for any 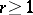 , only on the linear isotropy group
, only on the linear isotropy group 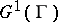 , and is called its
, and is called its  -th extension. A Lie pseudo-group of transformations
-th extension. A Lie pseudo-group of transformations 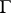 of order one is of finite type
of order one is of finite type 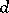 if and only if
if and only if
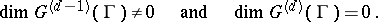 |
If, moreover, 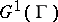 is irreducible, then
is irreducible, then 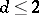 (cf. ). A Lie pseudo-group of transformations
(cf. ). A Lie pseudo-group of transformations 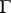 of order one is a pseudo-group of transformations of finite type only if, and in the complex case if and only if, the Lie algebra
of order one is a pseudo-group of transformations of finite type only if, and in the complex case if and only if, the Lie algebra 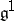 does not contain endomorphisms of rank 1 (cf. [10]). Such linear Lie algebras are called elliptic.
does not contain endomorphisms of rank 1 (cf. [10]). Such linear Lie algebras are called elliptic.
One has calculated the Lie algebras of all extensions 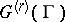 ,
, 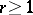 , where
, where 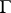 is a Lie pseudo-group of transformations of order one, in terms of the linear isotropy algebra. More precisely, the Lie algebra
is a Lie pseudo-group of transformations of order one, in terms of the linear isotropy algebra. More precisely, the Lie algebra 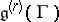 of
of 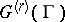 consists of the
consists of the 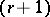 -jets of vector fields on
-jets of vector fields on 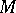 at
at 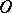 having, in some local coordinate system
having, in some local coordinate system 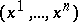 , the form
, the form
 |
where 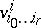 is an arbitrary tensor that is symmetric with respect to the lower indices and that satisfies the condition: For any fixed
is an arbitrary tensor that is symmetric with respect to the lower indices and that satisfies the condition: For any fixed 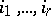 the matrix
the matrix
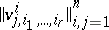 |
belongs to 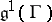 , relative to some coordinate system
, relative to some coordinate system 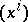 .
.
Let 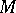 be an
be an  -dimensional differentiable manifold over the field
-dimensional differentiable manifold over the field 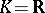 or
or 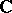 . Every transitive Lie pseudo-group of transformations
. Every transitive Lie pseudo-group of transformations 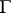 of order
of order 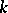 on a manifold
on a manifold 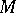 coincides with the pseudo-group of all local automorphism of some
coincides with the pseudo-group of all local automorphism of some  -structure (cf.
-structure (cf.  -structure) of order
-structure) of order 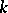 on
on 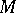 (Cartan's first fundamental theorem). The first classification of all primitive Lie pseudo-groups of infinite type was obtained by E. Cartan . According to his theorem, every primitive Lie pseudo-group of transformations of infinite type, consisting of holomorphic local transformations, is locally isomorphic to one of the pseudo-groups of Examples a)–f). This theorem has been repeatedly proved; its modern proofs lead to the study of certain filtered Lie algebras (cf. [9]). The classification of these filtered Lie algebras can be given on the basis of the classification of simple graded Lie algebras (cf. [3]). The classification of primitive pseudo-groups of transformations has also been obtained in the real case, and the condition of analyticity of the action of the pseudo-group of transformations has been replaced by the weaker condition of infinite differentiability (cf. [8], [9]). One has constructed certain abstract models of transitive Lie pseudo-groups, which came to play the same role in the theory of pseudo-groups of transformations of infinite type as do abstract Lie groups in the finite-dimensional case (cf. , [9]).
(Cartan's first fundamental theorem). The first classification of all primitive Lie pseudo-groups of infinite type was obtained by E. Cartan . According to his theorem, every primitive Lie pseudo-group of transformations of infinite type, consisting of holomorphic local transformations, is locally isomorphic to one of the pseudo-groups of Examples a)–f). This theorem has been repeatedly proved; its modern proofs lead to the study of certain filtered Lie algebras (cf. [9]). The classification of these filtered Lie algebras can be given on the basis of the classification of simple graded Lie algebras (cf. [3]). The classification of primitive pseudo-groups of transformations has also been obtained in the real case, and the condition of analyticity of the action of the pseudo-group of transformations has been replaced by the weaker condition of infinite differentiability (cf. [8], [9]). One has constructed certain abstract models of transitive Lie pseudo-groups, which came to play the same role in the theory of pseudo-groups of transformations of infinite type as do abstract Lie groups in the finite-dimensional case (cf. , [9]).
References
| [1] | S. Sternberg, "Lectures on differential geometry" , Prentice-Hall (1964) MR0193578 Zbl 0129.13102 |
| [2a] | E. Cartan, "Sur la structure des groupes infinis de transformations" , Oeuvres complètes , 2 , Gauthier-Villars (1953) pp. 571–624 MR1509054 MR1509040 Zbl 36.0223.03 Zbl 35.0176.04 |
| [2b] | E. Cartan, "Sur la structure des groupes infinis de transformations" , Oeuvres complètes , 2 , Gauthier-Villars (1953) pp. 625–714 MR1509054 MR1509040 Zbl 36.0223.03 Zbl 35.0176.04 |
| [2c] | E. Cartan, "Les groupes de transformations continus, infinis, simples" , Oeuvres complètes , 2 , Gauthier-Villars (1953) pp. 857–925 MR1509105 Zbl 40.0193.02 Zbl 38.0194.01 |
| [2d] | E. Cartan, "Les groupes de transformations continus, infinis, simples" , Oeuvres complètes , 2 , Gauthier-Villars (1953) pp. 1335–1384 MR1509105 Zbl 40.0193.02 Zbl 38.0194.01 |
| [3] | V. Guillemin, "Infinite dimensional primitive Lie algebras" J. Diff. Geom. , 4 : 3 (1970) pp. 257–282 MR0268233 Zbl 0223.17007 |
| [4] | S. Kobayashi, "Transformation groups in differential geometry" , Springer (1972) MR0355886 Zbl 0246.53031 |
| [5a] | S. Kobayashi, T. Nagano, "On filtered Lie algebras and geometric structures I" J. Math. Mech. , 13 : 5 (1964) pp. 875–907 MR0168704 Zbl 0142.19504 |
| [5b] | S. Kobayashi, T. Nagano, "On filtered Lie algebras and geometric structures III" J. Math. Mech. , 14 : 5 (1965) pp. 679–706 MR0188364 |
| [6a] | M. Kuranishi, "On the local theory of continuous infinite pseudo groups I" Nagoya Math. J. , 15 (1959) pp. 225–260 MR0116071 Zbl 0212.56501 |
| [6b] | M. Kuranishi, "On the local theory of continuous infinite pseudo groups II" Nagoya Math. J. , 19 (1961) pp. 55–91 MR0142694 Zbl 0212.56501 |
| [7] | P. Libermann, "Pseudogroupes infinitésimaux attachées aux pseudogroupes de Lie" Bull. Soc. Math. France , 87 : 4 (1959) pp. 409–425 MR123279 |
| [8] | S. Shnider, "The classification of real primitive infinite Lie algebras" J. Diff. Geom. , 4 : 1 (1970) pp. 81–89 MR0285574 Zbl 0244.17014 |
| [9] | I.M. Singer, S. Sternberg, "The infinite groups of Lie and Cartan. I. The transitive groups" J. d'Anal. Math. , 15 (1965) pp. 1–114 MR0217822 Zbl 0277.58008 |
| [10] | R.L. Wilson, "Irreducible Lie algebras of infinite type" Proc. Amer. Math. Soc. , 29 : 2 (1971) pp. 243–249 MR0277582 Zbl 0216.07401 |
Comments
References
| [a1] | C. Albert, P. Molino, "Pseudogroupes de Lie transitifs" , I–II , Hermann (1984–1987) MR0904048 MR0770061 Zbl 0682.53003 Zbl 0563.53027 |
| [a2] | J.F. Pommaret, "Systems of partial differential equations and Lie pseudogroups" , Gordon & Breach (1978) MR0517402 Zbl 0418.35028 Zbl 0401.58006 |
Pseudo-group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Pseudo-group&oldid=15959